...là ce matin je vois moins vaguement comment le faire mais (tant que je n'ai pas terminé c'est au conditionnel)
j'ai le RER à 6:00 du coup je ne pourrais pas terminer ce matin
bref!!
toujours dans la condition des modules

et

il fallait aussi démontrer que les modules

et pour tout
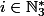
alors les modules

et

ça va vite puisque

vu que
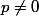
et les
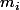
sont les racines de

et les
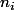
sont les racine de
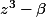
bon à partir de là on peut encore écrire autrement la formulation que l'on doit démontrer
si la formule (avec son extention par symétrie) est vraie alors

alors
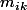
est une racine de

de même

alors
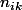
est une racine de

effectivement puisque

et comme

on a toujours

et


idem même chose pour arriver à

à partir de là ça devient plus chiant par contre avec les notations notamment
ci-dessous par exemple la notation

la lettre

n'est pas un indice
(elle fait partie du nom de la valeur que l'on définie)
par contre

est un indice
idem même remarque avec

,

,

,

et avec

,

,

,

,

bref on sait que (on le sait vu que c'est ce qui découle de la racine d'un polynôme de degré deux à coefficients complexes donc ça va le polynôme en question est écrit à la fin)
donc on sait qu'en posant
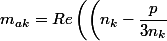^2+\dfrac {4p}{3}\right))
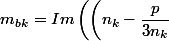^2+\dfrac {4p}{3}\right))

pour lorsque

sinon

bref

est le signe de

et en posant
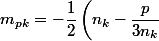+\dfrac {1}{2}\sqrt {\dfrac {\sqrt {m_{ak}^2+m_{bk}^2}+m_{ak}}{2}})

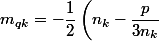-\dfrac {1}{2}\sqrt {\dfrac {\sqrt {m_{ak}^2+m_{bk}^2}+m_{ak}}{2}})

alors les

et

selon donc

sont les deux racines (pour chaque

donné) du polynôme
z-\dfrac {p}{3})
on pose idem
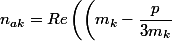^2+\dfrac {4p}{3}\right))
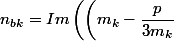^2+\dfrac {4p}{3}\right))

pour lorsque

sinon

et en posant
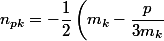+\dfrac {1}{2}\sqrt {\dfrac {\sqrt {m_{ak}^2+m_{bk}^2}+m_{ak}}{2}})

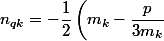-\dfrac {1}{2}\sqrt {\dfrac {\sqrt {n_{ak}^2+n_{bk}^2}+n_{ak}}{2}})

alors les

et

selon donc

sont les deux racines (pour chaque

donné) du polynôme
z-\dfrac {p}{3})
À partir de là je vois mieux comment conclure (mais bon c'est encore vague mais moins vague qu'à minuit)
mais là il est l'heure de prendre le RER (je verrais ce-soir)
