Isoler x dans une soustraction de racines carrées
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Mika
- Messages: 3
- Enregistré le: 18 Déc 2019, 11:29
-
 par Mika » 18 Déc 2019, 11:41
par Mika » 18 Déc 2019, 11:41
Bonjour à tous

Je souhaite isoler la valeur "x" de l'équation suivante.
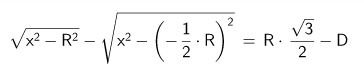
Malheureusement mes connaissances en mathématiques sont assez limités

et j'aurai besoin de votre aide.
Si quelqu'un peut m'expliquer comment faire, je lui en serai reconnaissant.
Merci

-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 18 Déc 2019, 12:16
par aymanemaysae » 18 Déc 2019, 12:16
Bonjour ;
Tu peux poser :
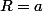
;
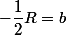
et
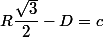
;
tu auras donc :
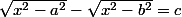
;
ensuite en élevant au carré , tu auras :
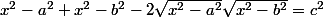
;
donc :
 = 2\sqrt{(x^2 - a^2)(x^2 - b^2)} = 2\sqrt{x^4 - (a^2 + b^2)x^2 + a^2b^2})
.
En posant

tu auras
x^2 + a^2b^2})
.
En élevant encore au carré , tu peux conclure rapidement .
Le problème peut se simplifier s'il y a une relation entre les valeurs des différentes variables .
-
Mika
- Messages: 3
- Enregistré le: 18 Déc 2019, 11:29
-
 par Mika » 18 Déc 2019, 12:26
par Mika » 18 Déc 2019, 12:26
Wahou, merci pour cette réponse ultra rapide

Non malheuresement par de rapports entres les R et D

Je vais tester tout cela et je vous tiens informé !
Merci encore !
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 18 Déc 2019, 12:31
par aymanemaysae » 18 Déc 2019, 12:31
De rien . Bon courage .
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 18 Déc 2019, 13:26
par pascal16 » 18 Déc 2019, 13:26
graphiquement, ça doit donner ça (vu le -1/2, je pense qu'à l’origine, les deux triangles ne sont pas du même coté ):
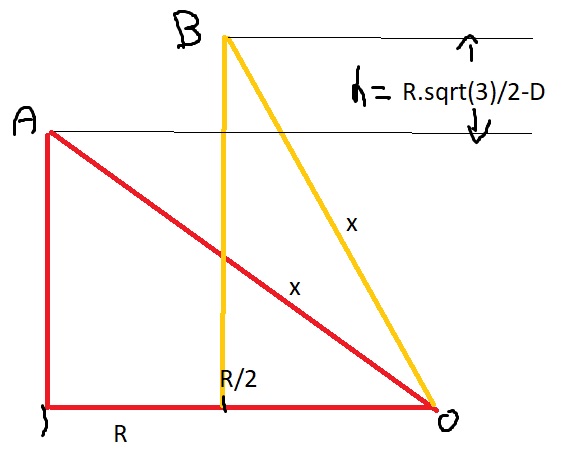
-
mathelot
 par mathelot » 18 Déc 2019, 14:01
par mathelot » 18 Déc 2019, 14:01
bonjour,

en multipliant par la quantité conjuguée (et en sautant quelques lignes de calcul):
})
on additionne les deux égalités (et après quelques calculs (on pensera à factoriser la différence de deux carrés)):
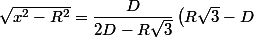)
en élevant au carré:
^2} \left(R\sqrt{3}-D\right)^2+R^2)
si x est positif
^2} \left(R\sqrt{3}-D\right)^2+R^2})
remarque: la quantité
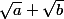
est conjuguée de
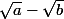
. Leur produit vaut a-b
Modifié en dernier par mathelot le 18 Déc 2019, 21:30, modifié 1 fois.
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 18 Déc 2019, 15:05
par aymanemaysae » 18 Déc 2019, 15:05
Pour voir si ce que j'ai présenté donne le même résultat que la méthode de Mathelot , j'élève au carré :
^2 = (2\sqrt{x^4 - (u^2 - c^2)x^2 + a^2b^2})^2)
,
ce qui donne :
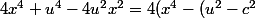x^2 + a^2b^2)= 4x^4 - 4(u^2 - c^2)x^2 +4 a^2b^2))
;
donc :

;
donc :
(u^2 + 2ab)}{4c^2})
.
Je laisse Mika vérifier l'égalité des deux résultats : bien sûr on a

et
R = -R^2)
.
-
mathelot
 par mathelot » 18 Déc 2019, 16:21
par mathelot » 18 Déc 2019, 16:21
j'ai fait un test avec des valeurs numériques, les deux formules donnent le même résultat.
-
Mika
- Messages: 3
- Enregistré le: 18 Déc 2019, 11:29
-
 par Mika » 18 Déc 2019, 21:06
par Mika » 18 Déc 2019, 21:06
Merci à tous pour votre !
Je vous met en lien une vidéo YouTube qui montre le mécanisme de la table Fletcher.
Pour information la valeur x correspond la corde des rayons en forme d’arc.
R la distance entre le centre de la table et l’extrémité du rayon fixée au disque.
D la distance d’un élément de la table entre le moment où elle totalement fermée et le moment où elle est totalement ouverte.
https://youtu.be/ppWxZLDjwEM
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 19 Déc 2019, 13:18
par aymanemaysae » 19 Déc 2019, 13:18
Bonjour ;
J'ai bien aimé la méthode de Mathelot et j'aimerai l'exploiter pour simplifier encore plus ma démarche :
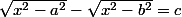
;
donc :
)
;
donc :
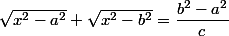
;
donc :
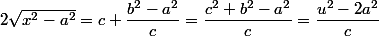
;
donc :
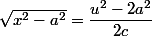
donc :
}{4c^2})
}{4c^2}=\dfrac{u^4-4a^2b^2-4a^2c^2}{4c^2})
;
donc :
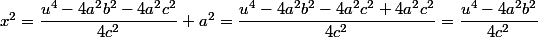
(u^2+2ab)}{4c^2})
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 87 invités
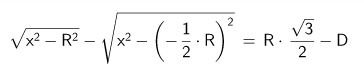
 et j'aurai besoin de votre aide.
et j'aurai besoin de votre aide.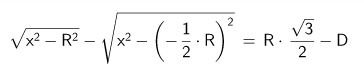
 et j'aurai besoin de votre aide.
et j'aurai besoin de votre aide.
