Irrationnelle racine

[upium666]

Bonjour à tous et à toutes !

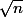
Dans un exercice, on souhaite étudier l'irrationalité de pour tout entier naturel
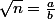
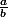
On suppose que avec une fraction irréductible, c'est à dire
On montre aisément que
Comment peut-on répondre à la problématique avec ce résultat ?

[Sylviel]

Et bien si n n'est pas un carré parfait, que peux tu dire ?

[upium666]

Et bien si n'est pas un carré parfait, que peux tu dire ?

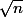
Si n'est pas un carré parfait, alors est irrationnel ?

[Robic]

Le plus simple, je pense, est d'utiliser la décomposition en facteurs premiers. Le fait que seuls les carrés parfaits ont une racine carrée entière saute alors aux yeux, non ?

[Ezra]

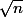
Si n'est pas un carré parfait, alors est irrationnel ?

On veut montrer que si un entier positif n'est pas un carré parfait, alors la racine de n'appartient pas à .
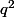
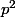
C'est le théorème de Gauss ( premier avec : ; si : , alors : . Ainsi ).