Inversion de fonctions circulaire
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
SPoke62
- Membre Relatif
- Messages: 128
- Enregistré le: 22 Juin 2007, 11:17
-
 par SPoke62 » 08 Oct 2007, 12:36
par SPoke62 » 08 Oct 2007, 12:36
Bonjour.
J'aurais besoin de quelques confirmations pour savoir si mes réponses sont correctes ou pas.
 = {\sqrt3 \over 2})
 : x = {\pi \over 6} + 2k\pi)
 : x = {5\pi \over 6} + 2k\pi)
--------------------------------------------------------------
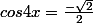
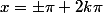
--------------------------------------------------------------
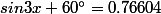

(1) : x = 3°20' + k120°
(2) : x = -23°20' + k120°
--------------------------------------------------------------
Merci
-
oscar
- Membre Légendaire
- Messages: 10024
- Enregistré le: 17 Fév 2007, 20:58
-
 par oscar » 08 Oct 2007, 15:07
par oscar » 08 Oct 2007, 15:07
Bonjour
1
sin (2x + pi/4) = v3/2 sin pi/3
2x +pi/4 = pi/3 +2kpi ou 2pi/3 +2kpi
2x = pi/3-pi/4 + 2kpi
2x = pi/12 +2kpî
x= pi/24 +kpi
2) cos 4x = - v2*2 = cos 3pi/4
4x = pi/4 +2kpi ou - pi/4 + 2kpi
x = pi/16 + 1/2 kpi ou -pi/16 + 1/2 kpi
3) ...???
-
SPoke62
- Membre Relatif
- Messages: 128
- Enregistré le: 22 Juin 2007, 11:17
-
 par SPoke62 » 08 Oct 2007, 16:12
par SPoke62 » 08 Oct 2007, 16:12
En fait j'avais tout faux quoi... :briques: :briques:
J'avais jamais vu ça de ma vie.
Comment est-ce que je pourrais construire les extrémités des arcs solutions sur un dessin?
Merci pour la correction.
je remets la 3) sin (3x +60°) = 0.76604 Et j'avais mis que 0.76604 c'était sin 50°
Et pour la 1) il manque la deuxième solution non?? 2x+pi/4 = 2pi/3 + 2kpi = 5pi/24 + kpi
-
SPoke62
- Membre Relatif
- Messages: 128
- Enregistré le: 22 Juin 2007, 11:17
-
 par SPoke62 » 08 Oct 2007, 17:34
par SPoke62 » 08 Oct 2007, 17:34
pour sin (3x +60°) = 0.76604
j'ai x = 3°20' + k120° ou x = -23°20' + k120°
C'est bon ou pas?
-
SPoke62
- Membre Relatif
- Messages: 128
- Enregistré le: 22 Juin 2007, 11:17
-
 par SPoke62 » 09 Oct 2007, 08:21
par SPoke62 » 09 Oct 2007, 08:21
 = cos ({7\pi \over 5} - x))
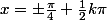
------------------------------------------------------------
 + tg (2x - {\pi \over 3}) = 0)

------------------------------------------------------------
 + sin (x + {\pi \over 12}) = 0)

ou
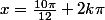
------------------------------------------------------------
tg x . tg 3x = 1

Qqn pourrait vérifier mes calculs svp ?
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 09 Oct 2007, 08:33
par Quidam » 09 Oct 2007, 08:33
oscar a écrit:Bonjour
1
sin (2x + pi/4) = v3/2 sin pi/3
2x +pi/4 = pi/3 +2kpi ou 2pi/3 +2kpi
2x = pi/3-pi/4 + 2kpi
2x = pi/12 +2kpî
x= pi/24 +kpi
2) cos 4x = - v2*2 = cos 3pi/4
4x = pi/4 +2kpi ou - pi/4 + 2kpi
x = pi/16 + 1/2 kpi ou -pi/16 + 1/2 kpi
3) ...???
Tu en as oublié la moitié en route...
1
sin (2x + pi/4) = v3/2 sin pi/3
2x +pi/4 = pi/3 +2kpi ou 2pi/3 +2kpi
2x = pi/3-pi/4 + 2kpi
2x = pi/12 +2kpî
x= pi/24 +kpi
ou
2x+pi/4=2pi/3+2kpi
2x=2pi/3-pi/4+2kpi
2x=5pi/12+2kpi
x=5pi/24+kpiQuant au 2), c'est inexact !
2) cos 4x = - v2*2 = cos 3pi/4
4x=3pi/4+2kpi
ou
4x=-3pi/4+2kpi
soit : x=3pi/16 +k(pi/2)
ou
x=-3pi/16+k(pi/2)
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 09 Oct 2007, 08:44
par Quidam » 09 Oct 2007, 08:44
SPoke62 a écrit:pour sin (3x +60°) = 0.76604
j'ai x = 3°20' + k120° ou x = -23°20' + k120°
C'est bon ou pas?
Non, c'est plutôt x=-(3°20')+k*120° ou x=23°20'+k*120°
Mais tu peux vérifier cela tout seul avec ta calculette !
Par exemple, si x=3,33333..., d'après toi, cela devrait marcher ! Vérifions !
sin((3x+60)°)=sin(70°)=0.9396 ... ca ne marche pas !
si x=-3.3333...+120 (une de mes solutions)
sin((3x+60)°)=sin((-10+360+60)°)=sin(50°) ça marche !
-
SPoke62
- Membre Relatif
- Messages: 128
- Enregistré le: 22 Juin 2007, 11:17
-
 par SPoke62 » 09 Oct 2007, 08:46
par SPoke62 » 09 Oct 2007, 08:46
La 1) j'avais complété dans une réponse.
Tu pourrais vérifier les dernières que j'ai poster s'il te plait??
OK pour sin (3x +60°) = 0.76604. Et merci pour la verif par calculatrice.
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 09 Oct 2007, 09:05
par Quidam » 09 Oct 2007, 09:05
SPoke62 a écrit: = cos ({7\pi \over 5} - x))
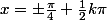
------------------------------------------------------------
 + tg (2x - {\pi \over 3}) = 0)

------------------------------------------------------------
 + sin (x + {\pi \over 12}) = 0)

ou
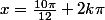
------------------------------------------------------------
tg x . tg 3x = 1

Qqn pourrait vérifier mes calculs svp ?
Je te donne le premier : je n'ai guère le temps de tout faire ! Il faut que tu vérifies à la calculette !
=\cos(\frac{7\pi}{5}-x))
Comme la solution de cos(a)=cos(b) est trouvée par
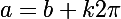
ou

, il est plus rapide de traiter les deux cas simultanément en posant

et en écrivant que les solutions sont données par
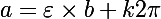
!
Donc :
=\cos(\frac{7\pi}{5}-x))
se traduit par :
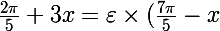+k2\pi)
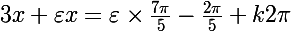
=\frac{\pi}{5}\times (7\varepsilon-2)+k2\pi)
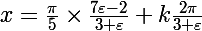
D'où, pour
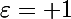
...
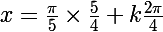
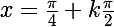
Celui là, tu l'avais trouvé !
Et pour
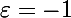
...
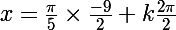
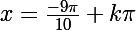
Mais pas celui-ci !
Courage !
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 09 Oct 2007, 09:12
par Quidam » 09 Oct 2007, 09:12
-
SPoke62
- Membre Relatif
- Messages: 128
- Enregistré le: 22 Juin 2007, 11:17
-
 par SPoke62 » 09 Oct 2007, 09:57
par SPoke62 » 09 Oct 2007, 09:57
 = cos 2x)
)
ca donne bien
 = sin ({\pi \over 2} + 2x))
sin A = sin B donne A = B + 2k

ou
A =

- B + 2k

Ce qui me donne :

ou
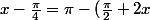 + 2k\pi)
C'est bon ou pas juque la?
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 09 Oct 2007, 10:01
par Quidam » 09 Oct 2007, 10:01
SPoke62 a écrit: = cos 2x)
)
ca donne bien
 = sin ({\pi \over 2} + 2x))
sin A = sin B donne A = B + 2k

ou
A =

- B + 2k

Ce qui me donne :

ou
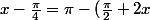 + 2k\pi)
C'est bon ou pas juque la?
Jusque là c'est bon !
-
SPoke62
- Membre Relatif
- Messages: 128
- Enregistré le: 22 Juin 2007, 11:17
-
 par SPoke62 » 09 Oct 2007, 10:02
par SPoke62 » 09 Oct 2007, 10:02
et je trouve

ou

-
SPoke62
- Membre Relatif
- Messages: 128
- Enregistré le: 22 Juin 2007, 11:17
-
 par SPoke62 » 10 Oct 2007, 07:38
par SPoke62 » 10 Oct 2007, 07:38
 = cos 2x)

ou

--------------------------------------------------------------------------
 + tg (2x - {\pi \over 3}) = 0)

-------------------------------------------------------------------------
 + sin(x + {\pi \over 12}) = 0)

ou
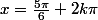
Voilà les trois dernières.
J'ai tout refait une par une.
Quelqu'un peut vérifier svp ?
Merci
-
SPoke62
- Membre Relatif
- Messages: 128
- Enregistré le: 22 Juin 2007, 11:17
-
 par SPoke62 » 11 Oct 2007, 09:24
par SPoke62 » 11 Oct 2007, 09:24
Comment fait-on pour construire sur le cercle trigonométrique les extrémités des arcs solutions???
Par exemple pour sin (3x +60°) = 0.76604
x=-(3°20')+k*120° ou x=23°20'+k*120°
Merci
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
