Inverse Pythagorean Theorem

[Pseuda]

Pour calculer la limite de , je ne vois rien d'immédiat dans les théorèmes connus : ce n'est pas une série, ni une série ou une suite de fonctions (quelles fonctions, quelle variable, et qui tend vers quoi ?), ni une somme double, je vois une simple suite indexée par , qui représente une somme de à pour les entiers impairs.

Cela doit pour voir se calculer, d'autant plus qu'on connaît la somme , en montrant que tend vers quand tend vers l'infini (en majorant les termes en ).

EDIT : Non, après essais, ce n'est pas si évident. Ce n'est même pas évident que cela soit vrai.

[Ben314]

Pour calculer la limite de , je ne vois rien d'immédiat dans les théorèmes connus...

Tout dépend où tu place le "connu", mais pour calculer partant du fait que les limites quand n->oo des trucs qu'on somme sont connus pour k fixé, ben c'est très exactement un problème de permutation limite/somme, c'est à dire un problème de permutation limite/intégrale avec la mesure de comptage.

Bref, tu écrit que où c'est l'ensemble des entiers (relatifs) impairs, c'est la mesure de comptage sur et est définie par si et sinon.
Ensuite, le fait que pour fixé , ben ça veut dire que la suite de fonction converge simplement vers la fonction .
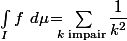
Et bien sûr, arrivé à ce point là, pour en déduire que la limite des , c'est , ben LE théorème qui vient à l'esprit, c'est évidement le théorème de convergence dominée de Lebesgue.
Et c'est pas super dur de montrer qu'il s'applique vu que pour k fixé, les sont nuls tant que , puis ensuite ils sont décroissant (évident sur un dessin) donc on a super facilement le sup (sur n) g(k) des et on vérifie facilement que g est intégrable pour (i.e. que la somme des g(k) est C.V.)

Mais bon, autant l'argumentaire est assez évident pour quelqu'un qui connaît la théorie de Lebesgue, autant pour un néophyte, le moins qu'on puisse dire, c'est que c'est tout sauf du hautement trivial ce truc là (faire comprendre le théorème de convergence dominé à un néophyte, je pense que c'est pas gagné...)
Et sinon, à mon avis, si on veut rester à un niveau en dessous de la théorie de Lebesgue, ben ça va être chaud de chez chaud de justifier la permutation limite/somme : on doit y arriver, mais c'est le type de truc où il faut "couper" le en des trucs bizarre du style les k tels que d'un coté et les autres k (qui vont compter pour du beurre) de l'autre.

[Pseuda]

Ok, merci Ben314. Je ne connaissais pas ce théorème, qui semble s'appliquer parfaitement ici. Finalement, cette "démonstration" vidéo n'est pas si géométrique qu'elle en a l'air. Le lien entre inverses carrés et pi a perdu un peu de son mystère, mais bon pas totalement, le lien n'est pas si immédiat.

Là où je trouve la vidéo décevante, c'est qu'il aurait fallu une étape de plus dans la construction des points, afin de mieux comprendre le passage à la généralité, et qu'on aurait pu se passer de toute la partie concernant les phares (en parlant directement des inverses des carrés des distances) qui embrouille au début plus qu'elle n'explique. Mais c'est mon point de vue, d'autres auront au contraire apprécié cette introduction.

Merci encore.