Introduire des entiers complexes : 1°) dans les équations di
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Djmaxgamer
- Membre Relatif
- Messages: 337
- Enregistré le: 27 Juin 2009, 12:43
-
 par Djmaxgamer » 16 Juil 2009, 23:14
par Djmaxgamer » 16 Juil 2009, 23:14
leon1789 a écrit:/(11+17i) \simeq 1.34 - 0.073 i)
on arrondit 1.34 à 1 et 0.073 à 0
et on prend q= 1+0i
Il vient 16+22i = (11+17i)q + r où r = 5+5i
et pgcd(16+22i, 11+17i) = pgcd(11+17i, 5+5i)
on continue :
/(5+5i) = 2.8 + 0.6 i)
on arrondit 2.8 à 3 et 0.6 à 1
et on prend q= 3+1.i
Il vient 11+17i = (5+5i)q + r où r = 1-3i
et pgcd(11+17i, 5+5i) = pgcd(5+5i, 1-3i)
a vous...
C'est un bon raisonnement ? Disons à préféré par rapport au graphique ? (l'arrondi des fractions)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 16 Juil 2009, 23:17
par Dinozzo13 » 16 Juil 2009, 23:17
:doh: , ça va trop vite, 'y a des messages de partout, je sais plus où on en est.
Pour commencer, est-ce que l'un de vous pourrait me rédiger une correction du 1er PGCD
\wedge{(3+4i)})
.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 16 Juil 2009, 23:19
par leon1789 » 16 Juil 2009, 23:19
Dinozzo13 a écrit::doh: , ça va trop vite, 'y a des messages de partout, je sais plus où on en est.
Pour commencer, est-ce que l'un de vous pourrait me rédiger une correction du 1er PGCD
\wedge{(3+4i)})
.
On sait que pgcd(5+5i, 3+4i)=pgcd(3+4i, 2+i)
Dinozzo13 a écrit:on recalcule pgcd(3+4i, 2+i) à la manière euclidienne !
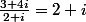
Soit B le point d'affixe z=2+1
non, z=2+1.i3+4i=z(2+i)+r'
r'=4i-2
en fait r'=0 Alors pgcd(5+5i , 3+4i) = pgcd(3+4i, 2+i) = pgcd(2+i,
0) = 2+i
Tu comprends, on arrondit les parties réels et imaginaires telles quelles...
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 16 Juil 2009, 23:22
par Dinozzo13 » 16 Juil 2009, 23:22
Moi, je vais me coucher, c'est pas une heure pour bosser ^^, à demain ^^.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 16 Juil 2009, 23:25
par leon1789 » 16 Juil 2009, 23:25
Djmaxgamer a écrit:Calculons pgcd(16+22i, 11+17i)
(...)
Alors pgcd(16+22i, 11+17i) = pgcd(11+17i, 5+5i)
(...)
Alors pgcd(11+17i, 5+5i)=pgcd(5+5i,1-3i)
(...)
Alors pgcd(5+5i,1-3i)=pgcd(1-3i,0)=1-3i
Donc : pgcd(16+22i, 11+17i) = 1-3i
exact !
Djmaxgamer a écrit:C'est un bon raisonnement ? Disons à préféré par rapport au graphique ? (l'arrondi des fractions)
Ta rédaction avec fraction est bonne. J'ai rédigé de manière plus "numérique"... mais on fait exactement la même chose en réalité.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 16 Juil 2009, 23:28
par leon1789 » 16 Juil 2009, 23:28
Dinozzo13 a écrit:Moi, je vais me coucher, c'est pas une heure pour bosser ^^, à demain ^^.
il faut simplement que tu penses à arrondir comme sur cet exemple
1.23 +
4.56 i s'arrondit en
1+
5 i
-
Djmaxgamer
- Membre Relatif
- Messages: 337
- Enregistré le: 27 Juin 2009, 12:43
-
 par Djmaxgamer » 16 Juil 2009, 23:30
par Djmaxgamer » 16 Juil 2009, 23:30
En fait la division donne un complexe z=a+ib et pour trouver le plus proche graphiquement, (et donc le quotient de la division euclidienne) il suffit d'arrondir a et b comme on a l'habitude de faire (à l'entier le plus proche)

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 16 Juil 2009, 23:31
par leon1789 » 16 Juil 2009, 23:31
En plus, il se trouve, que si on arrondit mal le quotient, par exemple on arrondit 1.23 + 4.56i en 2+4i , la division euclidienne se fait quand même et l'algo d'Euclide fonctionne toujours :zen:

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 16 Juil 2009, 23:36
par leon1789 » 16 Juil 2009, 23:36
leon1789 a écrit:Commençons par la division de 5+5i par 3+4i : on calcule
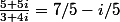
C'est un nombre complexe qui n'est pas dans Z[i], ok.
Dessiner dans R^2 le point d'affixe 7/5 - i/5 ,
et le point d'affixe a+ib (
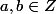
) le plus proche au sens de la distance habituelle. En clair, on arrondit 7/5 en
1 et -1/5 en
0.
Ainsi
q=1+0.i est l'entier de Gauss le plus proche (en distance) de

On termine la division euclidienne de 5+5i par 3+4i en posant
5+5i = q.(3+4i) + r
Comme q = 1, il vient r = 2+i
J'ai oublié de dire que q et r sont
quotient et reste de la division euclidienne de 5+5i par 3+4i.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 17 Juil 2009, 19:50
par Dinozzo13 » 17 Juil 2009, 19:50
Bonsoir, ce soir je n'ai pas beaucoup le temps d'être présent, j'espère donc que vous serez là demain ^^.
-
Djmaxgamer
- Membre Relatif
- Messages: 337
- Enregistré le: 27 Juin 2009, 12:43
-
 par Djmaxgamer » 17 Juil 2009, 19:58
par Djmaxgamer » 17 Juil 2009, 19:58
je suis la en tous cas quand tu veux ^^
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 18 Juil 2009, 12:28
par Dinozzo13 » 18 Juil 2009, 12:28
Djmaxgamer a écrit:je suis la en tous cas quand tu veux ^^
c'est super ^^, ça pouvait pas mieux tomber ^^.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 18 Juil 2009, 22:26
par Dinozzo13 » 18 Juil 2009, 22:26
Bonsoir, j'aimerais qu'on poursuive la division euclidienne dans Z[i].
petites questions :
- lorsqu'on cherche à calculer

avec
\in\mathbb{Z}[i]^{2})
, est-ce que l'on doit calculer obligatoirement
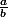
ou bien calculer on peut calculer
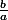
, c'est-à-dire, est-ce que l'ordre à une importance ?
- Lorsqu'on calcule
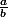
et qu'on tomble sur un élément de Z[i], est-ce que la division esst terminée ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 18 Juil 2009, 22:57
par Dinozzo13 » 18 Juil 2009, 22:57
Par exemple, j'ai essayé de déterminer
\wedge{(2+3i)})
.
J'ai commencé par calculer

mais pourrait-on aussi bien commencer par

?
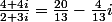
.
Comme

alors soit

tel que
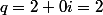
,

tel que:
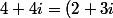q+r)
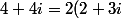+r)
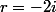
Donc
\wedge{(2+3i)}=(2+3i)\wedge{(-2i)})
.
Je fais de même,
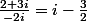
.
Comme

alors soit
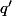
tel que
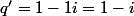
,

tel que:
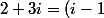q'+r')
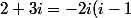+r')
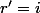
Donc
\wedge{(2+3i)}=(2+3i)\wedge{(-2i)}=(-2i)\wedge{(i)})
.
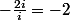
,

, donc
\wedge{(2+3i)}=(2+3i)\wedge{(-2i)}=(-2i)\wedge{(i)}=-2)
.
Donc
\wedge{(2+3i)}={-2})
.
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 19 Juil 2009, 07:20
par skilveg » 19 Juil 2009, 07:20
Je ne suis pas convaincu que
Dinozzo13 a écrit:\wedge{(i)}=-2)
ni que 2 divise

.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 19 Juil 2009, 08:39
par leon1789 » 19 Juil 2009, 08:39
Dinozzo13 a écrit:Par exemple, j'ai essayé de déterminer
\wedge{(2+3i)})
.
J'ai commencé par calculer

mais pourrait-on aussi bien commencer par

?
oui, pourquoi pas.
Dinozzo13 a écrit: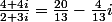
.
Comme

alors soit

tel que
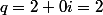
,

tel que:
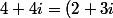q+r)
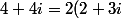+r)
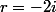
Donc
\wedge{(2+3i)}=(2+3i)\wedge{(-2i)})
.
ok
Avec l'autre fraction, on aurait pgcd(2+3i, 4+4i) = pgcd(4+4i,-2-i)
Dinozzo13 a écrit:Je fais de même,
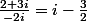
.
Comme

alors soit
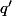
tel que
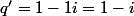
,

tel que:
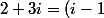q'+r')
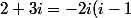+r')
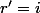
Donc
\wedge{(2+3i)}=(2+3i)\wedge{(-2i)}=(-2i)\wedge{(i)})
.
non, là, il y a coquille dans q', mais le reste est ok : on a bien
\wedge{(2+3i)}=(2+3i)\wedge{(-2i)}=(-2i)\wedge{(i)})
Or
\wedge{(i)} = 1)
...

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 19 Juil 2009, 08:39
par leon1789 » 19 Juil 2009, 08:39
Dinozzo13 a écrit: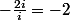
,

, donc
\wedge{(2+3i)}=(2+3i)\wedge{(-2i)}=(-2i)\wedge{(i)}=-2)
.
Donc
\wedge{(2+3i)}={-2})
.
et là, tu confonds le quotient et le reste !

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 19 Juil 2009, 08:45
par leon1789 » 19 Juil 2009, 08:45
Dinozzo13 a écrit:Par exemple, j'ai essayé de déterminer
\wedge{(2+3i)})
.
avec la première méthode par le module (juste pour dire qu'il est bon de connaitre les deux méthodes !), on a |4+4i|² = 32 et |2+3i|² = 13. Or pgcd(32, 13)=1 dans Z donc pgcd(4+4i, 2+3i)=1 dans Z[i].

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 19 Juil 2009, 08:49
par leon1789 » 19 Juil 2009, 08:49
Dinozzo13 a écrit:Par exemple, j'ai essayé de déterminer
\wedge{(2+3i)})
.
J'ai commencé par calculer

mais pourrait-on aussi bien commencer par

?
La réponse est oui, mais essaie de le justifier (c'est un bon exercice de compréhension). Conseil : singe la preuve que tu connais sur Z. N'oublie pas que le pgcd(a,b), c'est
le plus grand diviseur commun de a et b,
au sens de la divisibilité.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 19 Juil 2009, 15:58
par Dinozzo13 » 19 Juil 2009, 15:58
leon1789 a écrit:Or
\wedge{(i)} = 1)
...
Pourquoi ? si on simplifie par i, on a PGCD(-2i;i)=i
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 92 invités
