On cherche à résoudre l'équation (E) définie sur

par :
:(3-5i)x+(2+3i)y=1+i)
Prouvons tout d'abord l'existence de solutions. Pour cela, montrons que le pgcd de (3-5i) et de (2+3i) divise (2+i)
On appelle d ce pgcd.
Par définition,
 \\<br />d|(2+3i)<br />\end{array}<br />\right.)
Donc :
 \times (3+5i) \\<br />d|(2+3i) \times (2-3i)<br />\end{array}<br />\right.)


13 est un nombre premier. Il admet pour diviseurs

Or 34 n'est pas un multiple de 13.
On a alors

Ce n'est pas la méthode que vous avez employée, a savoir regarder le pgcd de 13 et 34, ce qui est, dans le cas général, bien sur plus juste, mais la je fais ce que j'ai fait par moi même
Or

mais j'aurais raisonné comme ca (plus chiant peut être mais :arf2: )
(1+i) étant évidemment divisible par 1, l'équation
)
admet des solutions dans

Cherchons un couple de solutions particulières
 \in \mathbb{Z})
de l'équation diophantienne
)
:34 \times u + 13 \times v = 1)
Comme vu précédemment,

donc
)
admet des solutions dans

Au passage cette vérification m'a l'air triviale : si on a montre auparavant que (E) avait des solutions, alors le pgcd de 34 et 13 divise 2. Donc soit l'equation est simplifiable (ce qu'il faut faire de suite, vu que le pgcd divise c, la simplification EST possible logiquement) et cette simplification amenera obligatoirement les deux coef. de la nouvelle equation diophantiennes premiers entre eux. Si il n'y a pas de simplification possible (comme ici, pgcd(34,13)=1) alors le pgcd est de 1 donc il y a des solutions. Plus globalement j'ai l'impression (sans l'avoir démontré (!!)) que si (E) admet des solutions, (E0) admet des solutions. Donc verification inutile ? (je pourrais essayer une démonstration j'ai le plan de la démo en tête mais je suis pas encore sur qu'elle tienne la route)... en gros : même si ca fait 2 lignes, c'est vraiment indispensable de montrer que E0 admet des solutions ?
Pour cela utilisons l'algorithme d'Euclide étendu :



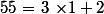
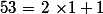
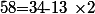
 = 13 \times 3 - 34)
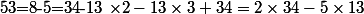

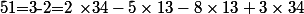

On a donc trouvé un couple de solutions particulières de l'équation diophantienne
)
:
)
Utilisons cette solution particulière pour trouver un couple
 \in \mathbb{Z}[i]^2)
solution particulière de
)
:(3-5i) \times u + (2+3i) \times v = 1)
Comme le couple
)
est solution de
)
on a :
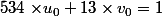
D'après les résultats précédents,
 \times (3+5i) \times u_0 + (2+3i) \times (2-3i) \times v_0=1)
Il suffit donc de poser :
 \times u_0 \\<br />v_0'= (2-3i) \times v_0<br />\end{array}<br />\right.)
On obtient :
 \\<br />v_0'= (-26+39i) <br />\end{array}<br />\right.)
Pour trouver une solution particulière de
)
on peut remarquer que :
 \times u_0' + (2+3i) \times v_0' = 1)
 \times ((3-5i) \times u_0' + (2+3i) \times v_0') = 1+i)
 \times (3-5i) \times u_0' + (1+i) \times (2+3i) \times v_0' = 1+i)
On obtient alors un couple
)
solution particulière de
)
si on pose :
 \times u_0'\\<br />v= (1+i) \times v_0'<br />\end{array}<br />\right.)
 \times (15+25i)\\<br />v= (1+i) \times (-26+39i)<br />\end{array}<br />\right.)
\\<br />v= (-65+13i)<br />\end{array}<br />\right.)
Et donc
)
est une solution particulière de
)
.
On obtient alors ce système de deux équations :
 \times x+(2+3i) \times y=1+i\\<br />(3-5i) \times (-10+40i)+(2+3i) \times (-65+13i)=1+i<br />\end{array}<br />\right.)
Par soustraction, on a :
 \times (x+10-40i)+(2+3i) \times (y+65-13i)=0)
 \times (x+10-40i)=(2+3i) \times (13i-65-y))
Comme
 \wedge (2+3i) = 1)
alors d'après le théorème de Gauss :
|(x+10-40i)\\<br />(3-5i)|(13i-65-y)<br />\end{array}<br />\right.)
Donc il existe
 \in \mathbb{Z})
tel que :
 = (x+10-40i)\\<br />k' \times (3-5i) = (13i-65-y)<br />\end{array}<br />\right.)
 - 10 + 40i\\<br />y= 13i-65-k' \times (3-5i)<br />\end{array}<br />\right.)
Montrons que k=k'
 \times x+(2+3i) \times y=1+i)
 \times (k \times (2+3i) - 10 + 40i)+(2+3i) \times (13i-65-k' \times (3-5i))=1+i)
 \times k \times (2+3i) +(3-5i) \times (- 10 + 40i)+(2+3i) \times (13i-65) - (2+3i) \times k' \times (3-5i)=1+i)
Or
)
est une solution particulière de
)
.
Donc
 \times (- 10 + 40i)+(2+3i) \times (13i-65)=1+i)
L'égalité devient :
 \times k \times (2+3i) - (2+3i) \times k' \times (3-5i)=0)
 \times (2+3i) \times (k-k')=0)
=0)

Les solutions de
)
sont donc :
 - 10 + 40i,13i-65-k \times (3-5i))|k\in\mathbb{Z}\})
ps : dsl du temps de recopiage...le TEX, c'est long...
