Intervalle et réunion d'intervalles, un vrai défis !

[Anonyme]

Bonjour
J'ai un exercice à faire, et j'ai quelques hésitations :
Voici tout d'abord l'énoncé :

Trouver tous les réels x qui vérifient chaque inégalité. Présente la réponse avec un intervalle ou une réunion d'intervalles.

PS : >= est égal à : supérieur ou égal à
et = 3
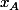
AM >= 3 avec =-2
x -3
Alors là je ne vois pas du tout !

Merci d'avance pour votre aide

[Anonyme]

Une réponse ? :id:

[MAC52]

Pour la 1) c'est x<=-5 ou x>=1
Pour la 2) c'est très simple: par définition une valeur absolue est positif: pour tout réel x, |x|>=0. Donc, pour tout réel x, |x|>=0>-3 d'où, pour tout réel x, |x|>-3.
Donc la réponse c'est R.

MAC

[Anonyme]

Merci mais je n'ai pas compris pourquoi c'était x<=-5 ou x>=1 et non pas x<=-5 ou x<=1, comment choisir le sens de l'égalité ?

et comment écrire avec la forme S={truc;truc} ?

[oscar]

Bonsoir

1) |-2-x| > = 3

Si -2-x > 0 ou -x > 2 ou x < -2 ,on a -2-x >=3; -x >= 5; x < = -5

si -2-x <0 ou x> -2, on a 2+x > = 3 ou x > = 1

S = x€ ]-oo; -5] U [ 1;+oo[

2) | x | > -3

Si x > 0 on a x > -3
Si,x <0, on a -x > -3 ou x <3

S = x € ] -3; 3 [