Intersection d'une hyperbole et d'une droite variable
15 messages
- Page 1 sur 1
 Intersection d'une hyperbole et d'une droite variable
Intersection d'une hyperbole et d'une droite variable
Bonjour à tous,
j'ai un DM pour vendredi (oui dès la rentrée haha) et j'ai vraiment des difficultés et ce depuis l'année dernière (actuellement en terminale S) voici le sujet, et je bloque d'emblée sur la question 1.
Soit f la fonction définie sur R \{-1} par f(x) = (2x+1)/(x+1) et H sa courbe représentative dans le plan muni d'un repère orthonormé (O;I;J)
1. Tacer H dans le repère ci-contre (comment tracer une courbe de ce type de fonction?)
2. Etudier le nombre de points d'intersection de H avec la droite D (y=x-2) et D' (y=x+4)
3. Etudier par le calcul la position relative de H et de D
Merci d'avance j'ai vraiment besoin d'aide.
j'ai un DM pour vendredi (oui dès la rentrée haha) et j'ai vraiment des difficultés et ce depuis l'année dernière (actuellement en terminale S) voici le sujet, et je bloque d'emblée sur la question 1.
Soit f la fonction définie sur R \{-1} par f(x) = (2x+1)/(x+1) et H sa courbe représentative dans le plan muni d'un repère orthonormé (O;I;J)
1. Tacer H dans le repère ci-contre (comment tracer une courbe de ce type de fonction?)
2. Etudier le nombre de points d'intersection de H avec la droite D (y=x-2) et D' (y=x+4)
3. Etudier par le calcul la position relative de H et de D
Merci d'avance j'ai vraiment besoin d'aide.
Re: Intersection d'une hyperbole et d'une droite variable
S'il ne s'agit que de tracer sa courbe représentative, n'importe quelle calculette ou logiciel de tracé fera l'affaire.
mais je pense qu'on te demande une étude détaillée de cette hyperbole : étude des variations, branches infinies, etc
mais je pense qu'on te demande une étude détaillée de cette hyperbole : étude des variations, branches infinies, etc
Re: Intersection d'une hyperbole et d'une droite variable
oui je l'ai tracer sur ma calculatrice mais il faut aussi la tracer sur le repère de ma feuille de DM et je n'y arrive pas ...
et non on ne me demande pasune étude aussi détaillée
et non on ne me demande pasune étude aussi détaillée
Re: Intersection d'une hyperbole et d'une droite variable
C'est vrai que ce pb est bizarre,
on ne te demande pas de démontrer
La courbe admet le point (-1,3) comme centre de symétrie
Trace les asymptotes et quelques points particuliers puis relie les entre eux
on ne te demande pas de démontrer
La courbe admet le point (-1,3) comme centre de symétrie
Trace les asymptotes et quelques points particuliers puis relie les entre eux
Re: Intersection d'une hyperbole et d'une droite variable
salut
une courbe est un ensemble de points dont les coordonnées x et y vérifient y = f(x)
que valent f(0), f(1) ? ... et tu places les points de coordonnées (0, f(0)), (1, f(1)) ... l'idéal étant de placer un maximum de points ...
et la calculatrice donne un tableau de valeurs ...
qu'as-tu appris en seconde ?
il n'est pas demander l'étude de f (du moins dans l'énoncé présenté ici) ...
une courbe est un ensemble de points dont les coordonnées x et y vérifient y = f(x)
que valent f(0), f(1) ? ... et tu places les points de coordonnées (0, f(0)), (1, f(1)) ... l'idéal étant de placer un maximum de points ...
et la calculatrice donne un tableau de valeurs ...
qu'as-tu appris en seconde ?
il n'est pas demander l'étude de f (du moins dans l'énoncé présenté ici) ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Intersection d'une hyperbole et d'une droite variable
oui je viens de tracer la courbe en utilisant cette méthode et je me suis aidé du tableur de ma calculatrice mais maintenant le problème est de trouver PAR LE CALCUL les points d'intersections avec les deux droites, je les ai déjà tracé et je sais déjà donc qu'il n'y a aucun point d'intersection de H avec D' mais il y en a 2 avec D, comment le prouver par le calcul?
Merci de votre réponse en tout cas.
Merci de votre réponse en tout cas.
Re: Intersection d'une hyperbole et d'une droite variable
M(x,y) sera un point d'intersection de H : y=(2x+1)/(x+1) et D : y =x-2) si ses coordonnées vérifient les 2 équation des 2 courbes soit (2x+1)/(x+1)=x-2
Re: Intersection d'une hyperbole et d'une droite variable
Pour tracer la courbe d'une fonction homographique =\frac{ax+b}{cx+d}) est vraiment très facile et tu n'a pas besoin de calculatrice pour cela. Une fois tu connais le principe, tu peux la tracer directement.
est vraiment très facile et tu n'a pas besoin de calculatrice pour cela. Une fois tu connais le principe, tu peux la tracer directement.
Prenons le cas général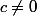
On trace dans le plan repère orthonormé (O;I;J)
On trace l'asymptote verticale
On trace l'asymptote horizontale
La courbe de f sera composée de deux courbes qui ne se touchent pas
Le plan est partagé par les deux asymptotes en 4 quadrants (le 1er quadrant correspondant à et
et  positifs)
positifs)
Nous avons=\dfrac{ad-bc}{\left (cx+d \right )^2})
Si les deux parties de la courbe se situent dans les quadrants 2 et 4
les deux parties de la courbe se situent dans les quadrants 2 et 4
Si les deux parties de la courbe se situent dans les quadrants 1 et 3
les deux parties de la courbe se situent dans les quadrants 1 et 3
On peut tracer juste une partie de la courbe, l'autre partie peut se déduire par symétrie de centre) point d'intersection des deux asymptotes. (On peut même tracer juste le quart de notre courbe en utilisant une autre symétrie par rapport à l'axe parallèle à la droite
point d'intersection des deux asymptotes. (On peut même tracer juste le quart de notre courbe en utilisant une autre symétrie par rapport à l'axe parallèle à la droite 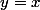 et passant par le centre de symétrie)
et passant par le centre de symétrie)
Prenons le cas général
On trace dans le plan repère orthonormé (O;I;J)
On trace l'asymptote verticale
On trace l'asymptote horizontale
La courbe de f sera composée de deux courbes qui ne se touchent pas
Le plan est partagé par les deux asymptotes en 4 quadrants (le 1er quadrant correspondant à
Nous avons
Si
Si
On peut tracer juste une partie de la courbe, l'autre partie peut se déduire par symétrie de centre
Re: Intersection d'une hyperbole et d'une droite variable
Razes a écrit:Pour tracer la courbe d'une fonction homographiqueest vraiment très facile et tu n'a pas besoin de calculatrice pour cela. Une fois tu connais le principe, tu peux la tracer directement.
Prenons le cas général
On trace dans le plan repère orthonormé (O;I;J)
On trace l'asymptote verticale
On trace l'asymptote horizontale
La courbe de f sera composée de deux courbes qui ne se touchent pas
Le plan est partagé par les deux asymptotes en 4 quadrants (le 1er quadrant correspondant àet
positifs)
Nous avons
Siles deux parties de la courbe se situent dans les quadrants 2 et 4
Siles deux parties de la courbe se situent dans les quadrants 1 et 3
On peut tracer juste une partie de la courbe, l'autre partie peut se déduire par symétrie de centrepoint d'intersection des deux asymptotes. (On peut même tracer juste le quart de notre courbe en utilisant une autre symétrie par rapport à l'axe parallèle à la droite
et passant par le centre de symétrie)
tu rêves là ... penser qu'un élève de terminale est capable de penser et savoir cela ....
et l'histoire des quadrants est un savoir inutile ... (comme pour le second degré je préfère connaître la forme canonique qui donne tout)
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Intersection d'une hyperbole et d'une droite variable
merci beaucoup pour vos réponses mais zygomatique a raison je n'ai pas encore appris tout cela haha mais je prend note, merci
Re: Intersection d'une hyperbole et d'une droite variable
very easy de tracer la courbe de f ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Intersection d'une hyperbole et d'une droite variable
oui merci je l'ai tracé comme ça c'était simple finalement haha
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
