Bonjour,
Après avoir retravaillé les primitives des fonctions usuelles, j'ai remarqué que les ensembles de définition des fonctions à primitiver coïncidaient tout le temps avec l'intervalle sur lequel les primitives étaient dérivables (je parle de la colonne "intervalle" que l'on peut trouver dans plusieurs tables de primitives). Est-ce toujours le cas?
Merci beaucoup d'avance pour vos éclaircissements!
Interrogation sur les primitives
7 messages
- Page 1 sur 1
Re: Interrogation sur les primitives
J'en profite au passage pour poser une autre question : dans la définition même de la primitive d'une fonction on précise toujours que cette fonction est continue sur l'intervalle d'étude... pourquoi cette condition?
Re: Interrogation sur les primitives
Agassi a écrit:Bonjour,
Après avoir retravaillé les primitives des fonctions usuelles, j'ai remarqué que les ensembles de définition des fonctions à primitiver coïncidaient tout le temps avec l'intervalle sur lequel les primitives étaient dérivables (je parle de la colonne "intervalle" que l'on peut trouver dans plusieurs tables de primitives). Est-ce toujours le cas?
Merci beaucoup d'avance pour vos éclaircissements!
Il serait plus juste d'utiliser le terme "Intégrer" plutot que "Primitiver", ensuite ce n'est pas forcément toujours le cas.
On peut prendre, par exemple
Agassi a écrit:J'en profite au passage pour poser une autre question : dans la définition même de la primitive d'une fonction on précise toujours que cette fonction est continue sur l'intervalle d'étude... pourquoi cette condition?
Cela n'est pas vraiment dans la définition d'une primitive, a ma connaissance. La primitive d'une fonction est une fonction, qui, dérivée, donne la fonction dont elle est la primitive. (Le contraire de la dérivation)
Or les primitives sont beaucoup utilisées pour manipuler les intégrales, et lorsqu'on calcule une intégrale il est demandé que la fonction soit continue sur l'intervalle demandé pour que le résultat soit pertinent.
En espérant que cela réponde a ta question !
Re: Interrogation sur les primitives
Kugge a écrit:On peut prendre, par exemplequi a comme primitive
or
est défini sur
et
est défini uniquement sur
.
Puis-je faire remarquer qu'une primitive de
Re: Interrogation sur les primitives
GaBuZoMeu a écrit:Puis-je faire remarquer qu'une primitive deest
, qui est bien défini sur
?
Au niveau fin terminale nous n'avons pas vu cela, mais toute information est bonne à prendre
Re: Interrogation sur les primitives
Remarque culturelle supplémentaire : il n'est pas nécessaire qu'une fonction soit continue pour calculer son intégrale (même si ça facilite grandement les choses). Le cas le plus courant est lorsque la fonction  est continue par morceaux comme la fonction partie entière par exemple dont l'intégrale est parfaitement définie. On peut aussi penser à des monstres mathématiques un peu plus subtiles comme la fonction caractéristique des rationnels définie par :
est continue par morceaux comme la fonction partie entière par exemple dont l'intégrale est parfaitement définie. On peut aussi penser à des monstres mathématiques un peu plus subtiles comme la fonction caractéristique des rationnels définie par :
=\left\{\begin{aligned} &1 &\text{ si } x\in\mathbb{Q} \\ &0 &\text{ sinon}\end{aligned}\right.)
Dans ce cas là tout dépend de la définition de l'intégrale qu'on utilise, au lycée on utilise l'intégrale de Riemann (que l'on peut voir comme une application de la méthode des rectanges) et dans ce cas là l'intégrale n'a aucun sens puisque la fonction n'est pas intégrable. En revanche l'intégrale de Lebesgue permet de donner un sens à son intégrale qui est alors nulle. Concernant le domaine de définition des primitives, si on définit une primitive d'une fonction
une primitive d'une fonction  quelconque alors
quelconque alors  doit être dérivable là où
doit être dérivable là où  est définie, plutôt que d'appeler
est définie, plutôt que d'appeler  une primitive de
une primitive de  on peut de façon plus précise définir
on peut de façon plus précise définir  comme une primitive de
comme une primitive de  sur
sur  . Par exemple la fonction
. Par exemple la fonction 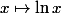 est une primitive de
est une primitive de 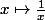 sur
sur 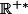 et
et  est une primitive de
est une primitive de 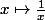 sur
sur 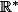 .
.
Dans ce cas là tout dépend de la définition de l'intégrale qu'on utilise, au lycée on utilise l'intégrale de Riemann (que l'on peut voir comme une application de la méthode des rectanges) et dans ce cas là l'intégrale n'a aucun sens puisque la fonction n'est pas intégrable. En revanche l'intégrale de Lebesgue permet de donner un sens à son intégrale qui est alors nulle. Concernant le domaine de définition des primitives, si on définit
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 87 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
