salut !
une preuve ?
MERCI
Interprétation geométrique du PGCD
8 messages
- Page 1 sur 1
sue a écrit:pour etre plus claire :
comment puis-je montrer que pgcd(a.b) = le nombre de points à coordonée entières appartenant à [OM] , tq M(a,b) et O(0,0) ??
Ben, si tu commençais avec :
Soit a',b' un point à coordonnées entières de [OM]. Alors,
M'étonnerait bien que tu n'arrives pas au bout...
M'étonnerait bien que tu n'arrives pas au bout...
en pleines vaccances tt est possible :zen:
i.e il suffit de déterminer le nb de solution de cette équation t.q a,b,a',b' entiers nat.
on a a|ba' donc
si a et b sont premiers entre eux , il ya une seule façon de choisir k .
si b|a alors il y a exactement b façon de choisir k (puisque K est inf à
sinon (b ne divise pas a) je vois pas comment l'exprimer , mais le résultat me semble évident juste en dénombrant. :triste:
c'est grave docteur ?
Bonjour 
bon ok ça motive :we: mais en pleines vaccances on sait jamais ...
"" ""
""
ok . posons , on a
, on a 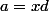 et
et 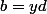 tq
tq .
.
on a donc soit xb'=ya' (on compte pas la solution triviale (0,0))
soit xb'=ya' (on compte pas la solution triviale (0,0))
soit : et
et  , Gauss me permet de conclure ;
, Gauss me permet de conclure ;  tq
tq  et
et  , donc il y a exactement
, donc il y a exactement  façons de choisir
façons de choisir  (puisque a' et b' sont resp. inf ou = à a et b ) on obtient ainsi
(puisque a' et b' sont resp. inf ou = à a et b ) on obtient ainsi  couples
couples .)
ça marche ?

M'étonnerait bien que tu n'arrives pas au bout...
bon ok ça motive :we: mais en pleines vaccances on sait jamais ...
""
ok . posons
on a donc
soit :
ça marche ?
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
