Integrales
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Inogood
- Membre Naturel
- Messages: 64
- Enregistré le: 09 Nov 2011, 13:32
-
 par Inogood » 08 Avr 2012, 09:14
par Inogood » 08 Avr 2012, 09:14
Bonjour,
Je suis bloque a un exercice :
On pose, pour tout enter n naturel :
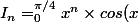dx)
A/ Prouver que

B/ Quelle est la limite de
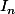
?
===== Ce que j'ai fait :
A/


)
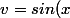)
je fais le calcul d'integrales et je tombe sur :
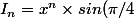 - n(x^{n-1} \times sin(\pi / 4 )))
Que faire ? Toute aide sera appréciée !
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 08 Avr 2012, 09:34
par vincentroumezy » 08 Avr 2012, 09:34
Inogood a écrit:Bonjour,
Je suis bloque a un exercice :
On pose, pour tout enter n naturel :
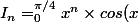dx)
A/ Prouver que

B/ Quelle est la limite de
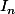
?
===== Ce que j'ai fait :
A/


)
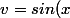)
je fais le calcul d'integrales et je tombe sur :
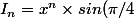 - n(x^{n-1} \times sin(\pi / 4 )))
Que faire ? Toute aide sera appréciée !
Bonjour.
Déjà, montrer la positivité de l'intégrale est rapide, car ta
)
est positif sur l'intervalle considéré, et que les bornes sont dans l'ordre.
Pour majorer l'intégrale, cherches à quel réel ta fonction est toujours inférieure sur l'intervalle.
-
Inogood
- Membre Naturel
- Messages: 64
- Enregistré le: 09 Nov 2011, 13:32
-
 par Inogood » 08 Avr 2012, 10:11
par Inogood » 08 Avr 2012, 10:11
vincentroumezy a écrit:Bonjour.
Déjà, montrer la positivité de l'intégrale est rapide, car ta
)
est positif sur l'intervalle considéré, et que les bornes sont dans l'ordre.
Pour majorer l'intégrale, cherches à quel réel ta fonction est toujours inférieure sur l'intervalle.
Je ne vois vraiment pas comment m'y prendre...
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 08 Avr 2012, 10:13
par vincentroumezy » 08 Avr 2012, 10:13
Entre O et Pi/4, quel est le maximum de x ?
-
Inogood
- Membre Naturel
- Messages: 64
- Enregistré le: 09 Nov 2011, 13:32
-
 par Inogood » 08 Avr 2012, 10:28
par Inogood » 08 Avr 2012, 10:28
vincentroumezy a écrit:Entre O et Pi/4, quel est le maximum de x ?
x prend une valeur de Pi/4 car In est sur l'intervale [0;pi/4], pi/4 etant le maximum.
Donc ca c'est pour In.
Apres faut prendre f(x) et dire son maximum et dire qu'il est superieur a celui de In ?
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 08 Avr 2012, 10:31
par vincentroumezy » 08 Avr 2012, 10:31
Tu sais maintenant que
dx=\frac{\pi}{4}^n \int_0^{\frac{\pi}{4}} cos(x))
, qui vaut....
-
Inogood
- Membre Naturel
- Messages: 64
- Enregistré le: 09 Nov 2011, 13:32
-
 par Inogood » 08 Avr 2012, 10:42
par Inogood » 08 Avr 2012, 10:42
vincentroumezy a écrit:Tu sais maintenant que
dx=\frac{\pi}{4}^n \int_0^{\frac{\pi}{4}} cos(x))
, qui vaut....
= [F(pi/4) -F(0)]*pi/4^n
= [sin(pi/4) - sin (0)]*pi/4^n
= environ 0,71*pi/4^n
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 08 Avr 2012, 10:47
par vincentroumezy » 08 Avr 2012, 10:47
sin(Pi/4), ça vaut combien ?
Et sin(0) ?
-
Inogood
- Membre Naturel
- Messages: 64
- Enregistré le: 09 Nov 2011, 13:32
-
 par Inogood » 08 Avr 2012, 10:49
par Inogood » 08 Avr 2012, 10:49
sin(pi/4)=cos(pi/4)
sin(0)=0
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 08 Avr 2012, 10:52
par globule rouge » 08 Avr 2012, 10:52
Inogood a écrit:sin(pi/4)=cos(pi/4)
sin(0)=0
C'est bon, tu as ton encadrement

Julie
-
Inogood
- Membre Naturel
- Messages: 64
- Enregistré le: 09 Nov 2011, 13:32
-
 par Inogood » 08 Avr 2012, 11:20
par Inogood » 08 Avr 2012, 11:20
globule rouge a écrit:C'est bon, tu as ton encadrement

Julie
Et pour la limite de la suite, comment je fais ? Lim pi/4^n (cos(pi/4)) quand n = quoi?
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 08 Avr 2012, 12:23
par globule rouge » 08 Avr 2012, 12:23
Inogood a écrit:Et pour la limite de la suite, comment je fais ? Lim pi/4^n (cos(pi/4)) quand n = quoi?
Si tu as bien
^n)
, tu peux facilement utiliser le théorème des gendarmes puisque

!

-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 08 Avr 2012, 12:49
par vincentroumezy » 08 Avr 2012, 12:49
Inogood a écrit:Et pour la limite de la suite, comment je fais ? Lim pi/4^n (cos(pi/4)) quand n = quoi?
Quand n tend vers l'infini (comme toujours pour une suite).
-
Mooni93
- Messages: 9
- Enregistré le: 05 Avr 2012, 21:13
-
 par Mooni93 » 08 Avr 2012, 12:52
par Mooni93 » 08 Avr 2012, 12:52
vincentroumezy a écrit:Bonjour.
Déjà, montrer la positivité de l'intégrale est rapide, car ta
)
est positif sur l'intervalle considéré, et que les bornes sont dans l'ordre.
Pour majorer l'intégrale, cherches à quel réel ta fonction est toujours inférieure sur l'intervalle.
quel logiciel tu utilise afin de pouvoir ecrire en symboles mathematiques comme tu l'a fait svp
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 08 Avr 2012, 12:56
par vincentroumezy » 08 Avr 2012, 12:56
Mooni93 a écrit:quel logiciel tu utilise afin de pouvoir ecrire en symboles mathematiques comme tu l'a fait svp
Aucun, c'est simplement du LaTeX.
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 08 Avr 2012, 13:34
par globule rouge » 08 Avr 2012, 13:34
Mathématique divine a écrit::hum: :doh:
Je suis impressionnée! Comment pouvez-vous comprendre ceci?
Ne t'inquiète pas, c'est très facile !! Si tu veux il y a une page pour que tu apprennes les bases sur le forum lycée

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
?


)
est positif sur l'intervalle considéré, et que les bornes sont dans l'ordre.
est positif sur l'intervalle considéré, et que les bornes sont dans l'ordre.