Intégrale et valeur absolue

par **mateo49** » 29 Oct 2009, 10:53

Bonjour,
J'ai un problème de signe dans mon résultat et je trouve pas mon erreur.

Donc:

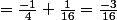
Alors que normalement je devrais trouver

Quelqu'un peu m'aider? :help:

par **le_fabien** » 29 Oct 2009, 11:19

mateo49 a écrit:Bonjour,
J'ai un problème de signe dans mon résultat et je trouve pas mon erreur.

Donc:

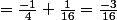
Alors que normalement je devrais trouver
Quelqu'un peu m'aider? :help:

Bonjour,
normal il faut supprimer la valeur absolue avant de calculer l'integrale.
Et dans [1;2] lx²-2xl=-x²+2x

par **mateo49** » 29 Oct 2009, 11:26

Tu es sûr cette fois, car ca me parait bizarre.

par **mateo49** » 29 Oct 2009, 15:44

Personne peut m'aider, je bloque :mur: ca fait mal

par **dudumath** » 29 Oct 2009, 15:45

si x est compris entre 1 et 2, quel est le signe de x²-2x??

par **mateo49** » 29 Oct 2009, 15:47

Il est négatif et alors?

par **benekire2** » 29 Oct 2009, 15:52

et alors tu prend l'opposé comme ca c'est positif et le tour est joué!!

par **mateo49** » 29 Oct 2009, 16:02

Merci les gars j'ai enfin compriiiiiiiiiiiiiiiiiiiiiiii
cool

par **mateo49** » 29 Oct 2009, 16:25

Et si l'intervalle de travail est [x>2;1], comment faire dans ce cas la?
Je ne peux pas changer la fonction au debut car la valeur absolue est positive ou négative.

par **benekire2** » 29 Oct 2009, 16:26

Les maths c'est facile quand on a compris^^

par **mateo49** » 29 Oct 2009, 16:41

Non plus personne pour mon dernier problème?

par **le_fabien** » 29 Oct 2009, 17:27

mateo49 a écrit:Et si l'intervalle de travail est [x>2;1], comment faire dans ce cas la?
Je ne peux pas changer la fonction au debut car la valeur absolue est positive ou négative.

Je ne comprends pas trop ta question. :triste:

par **mateo49** » 30 Oct 2009, 08:17

Oui alors ma question est que je dois aussi calculer:

Sachant que m>2

Donc la je ne peux pas utiliser la méthode précédente car dans l'intervalle la valeur absolue peut etre positive ou négative. :hum:

par **mateo49** » 30 Oct 2009, 09:30

Vraiment personne ne peut m'aider???????
Je tourne en rond :happy:

par **le_fabien** » 30 Oct 2009, 11:08

Et bien tu coupes ton integrale en deux.
Une de 1 à 2 et l'autre de 2 à m.
Tu additionnes les deux .

par **mateo49** » 30 Oct 2009, 11:36

Ca a l'aire si simple quand tu dis ca :we:
je vais essayé :crunch:

par **le_fabien** » 30 Oct 2009, 17:05

mateo49 a écrit:Ca a l'aire si simple quand tu dis ca :we:
je vais essayé :crunch:

C'est très simple !! :zen:

Intégrale et valeur absolue

Intégrale et valeur absolue

Qui est en ligne