Intégrale
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
anerdygirl
- Messages: 7
- Enregistré le: 28 Déc 2020, 13:37
-
 par anerdygirl » 14 Fév 2021, 19:33
par anerdygirl » 14 Fév 2021, 19:33
bonsoir, voici un problème que je n'arrive pas à résoudre:
3) soit
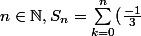^k \frac{1}{2k+1})
et
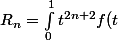dt)
a. montrer que
=\sum_{k=0}^{n}(-1)^k(\frac{1}{\sqrt{3}})^{2k}+(\frac{-1}{\sqrt{3}})^{n+1}t^{2n+2}f(t))
b. en déduire que
^{n+1}R_n=\frac{\pi}{2\sqrt{3}})
c. montrer que

puis déduire la limite de

donnée:
=\frac{3}{3+x^2})
merci d'avance
-
Rdvn
- Habitué(e)
- Messages: 840
- Enregistré le: 05 Sep 2018, 11:55
-
 par Rdvn » 15 Fév 2021, 18:59
par Rdvn » 15 Fév 2021, 18:59
Bonjour
1)Êtes vous bien sûr(e) d'avoir bien transcrit l'énoncé ?
Relisez la question a)...
2)Vous êtes en rubrique Lycée , ne serait ce pas Supérieur ?
A vous lire
Cdlt
-
mathelot
 par mathelot » 15 Fév 2021, 21:29
par mathelot » 15 Fév 2021, 21:29
bonsoir,
nous allons utiliser
la formule de somme des termes d'une progression géométriquesoit q la raison ,
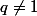
, il vient

d'où
 (*)
(*)comme on a :
=\dfrac{1}{1+(\frac{x}{\sqrt{3}})^2})
pour résoudre la question (3.a)
on peut appliquer la formule (*) avec
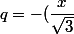^2)
remarque: l'énoncé de la question (3.a) comporte deux erreurs.
-
Rdvn
- Habitué(e)
- Messages: 840
- Enregistré le: 05 Sep 2018, 11:55
-
 par Rdvn » 15 Fév 2021, 22:57
par Rdvn » 15 Fév 2021, 22:57
En effet, c'est bien ce que j'en pensais.
Suivant la charte de ce forum, il me semblait utile d'amener d'abord anerdygirl à rectifier ses erreurs d'énoncés, afin pouvoir ensuite lui donner une première indication.
D'où ma première réponse.
-
anerdygirl
- Messages: 7
- Enregistré le: 28 Déc 2020, 13:37
-
 par anerdygirl » 18 Fév 2021, 15:48
par anerdygirl » 18 Fév 2021, 15:48
Bonjour Rdvn,
tout d'abord je m'excuse pour la réponse tardive. Vous avez bien raison, il y avait un faute de frappe dont ma prof ne s'est pas rendu compte, et moi non plus.
il s'agit de ^{n+1}) au niveau de la première question.
au niveau de la première question.de plus je suis encore en lycée, c'est juste que je ne suis pas le programme français.
-
Rdvn
- Habitué(e)
- Messages: 840
- Enregistré le: 05 Sep 2018, 11:55
-
 par Rdvn » 18 Fév 2021, 19:30
par Rdvn » 18 Fév 2021, 19:30
Bonsoir
En effet c'était l'une des erreurs, l'autre est que c'est
(t/rc(3))^2k
et non
(1/rc(3))^2k comme marqué
vous pouvez d'ailleurs remarquer que
(t/rc(3))^2k=( (t^2)/3 )^k
et là l'indication que mathelot vous a donnée vous permet de venir à bout du a
Puis à suivre
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 88 invités