Intégrale et symétrie [résolu]

[t.itou29]

Bonsoir,
Je chercher à prouver par le calcul un problème dont j'ai trouvé la solution graphiquement:

Calculer :

En traçant la fonction on remarque que I est égale à la moitié du rectangle de côté , le problème est de le prouver !

Par le calcul "bourrin" en utilisant cotan(x) (les courbes sont "symétriques") et par changement de variable ça le fait mais ça oblige de se soucier de la continuité et c'est relativement long ... Auriez-vous une astuce ?

EDIT: j'ai trouvé la correction et finalement il n'y avait pas plus simple

[chan79]

salut
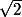
Je remplacerais par k.
La fonction f à intégrer est prolongeable par continuité en .
Montre que
Intègre de 0 à pi/4 puis de pi/4 à pi/2

[t.itou29]

salut
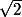
Je remplacerais par k.
La fonction f à intégrer est prolongeable par continuité à gauche en .
Montre que
Intègre de 0 à pi/4 puis de pi/4 à pi/2

Oui c'est ce que j'ai fait sauf que j'ai utilisé un changement de variable pour montrer que integrale f(x)=integrale f(pi/2-x) ce qui rallonge les calculs. En découpant l'intégrale comme vous le faites c'est plus rapide ! Merci