Intégrale pourquoi F(x) borné de x à a doit s'annuler en a?
15 messages
- Page 1 sur 1
Intégrale pourquoi F(x) borné de x à a doit s'annuler en a?
Bonjour, alors attention, je précise l'annulation ne concerne pas cette banalité d'usage des intégrales quand on remplace dans ce cas x par a et qu'on a un double-bornage en a, ce qui conduit bien sûr à une annulation, je voulais savoir pourquoi dans cette forme d'intégrale écrite à l'aide d'une primitive on exige que celle-ci s'annule en a(c'est-à-dire le bornage du bas uniquement) alors que dans le cas de f(b)-f(a) , on ne demande pas à ce que la primitive s'annule en a, pourquoi cette exigence?
PS: pour ceux qui n'ont pas compris la question , merci de m'épargner vos commentaires négatifs du type"tu confonds intégrale et primitives bla bla"
PS: pour ceux qui n'ont pas compris la question , merci de m'épargner vos commentaires négatifs du type"tu confonds intégrale et primitives bla bla"
- Fichiers joints
-
- Sans titre.png (24.84 Kio) Vu 2584 fois
Re: Intégrale pourquoi F(x) borné de x à a doit s'annuler e
Bonsoir,
F s'annule effectivement en a et c'est en effet la seule primitive de f qui vérifie cela, c'est assez facile a montrer. On exige pas que F s'annule en a, on le constate, on le prouve. Mais je ne suis pas sur d'avoir compris le sens de ta question.
Pas la peine non plus d'être agressif.
F s'annule effectivement en a et c'est en effet la seule primitive de f qui vérifie cela, c'est assez facile a montrer. On exige pas que F s'annule en a, on le constate, on le prouve. Mais je ne suis pas sur d'avoir compris le sens de ta question.
Pas la peine non plus d'être agressif.
Borne sup, maths spé !
Re: Intégrale pourquoi F(x) borné de x à a doit s'annuler e
salut
MDR (je suis désolé mais vu ton discours je ne peux m'en empécher ...)
on n'exige pas : c'est un fait : combien vaut = \int_a^a f(t)dt) ?
?
d'autre part G(x) = F(x) + k est une autre primitive de f puisque G'(x) = F'(x) = f(x)
donc si k <> 0 alors G(a) <> 0 et donc F est une primitive qui s'annule en a et si k = 0 alors F = G donc F est unique
réciproquement notons maintenant H une primitive quelconque de f alors par définitiondt = [H(t)]_a^x = H(x) - H(a)) donc
donc  = H(a) + \int_a^x f(t)dt) et cet intégrale est nulle lorsque x = a
et cet intégrale est nulle lorsque x = a
donc H(a) = H(a) + 0 = 0 <=> H(a) = 0
...
MDR (je suis désolé mais vu ton discours je ne peux m'en empécher ...)
on n'exige pas : c'est un fait : combien vaut
d'autre part G(x) = F(x) + k est une autre primitive de f puisque G'(x) = F'(x) = f(x)
donc si k <> 0 alors G(a) <> 0 et donc F est une primitive qui s'annule en a et si k = 0 alors F = G donc F est unique
réciproquement notons maintenant H une primitive quelconque de f alors par définition
donc H(a) = H(a) + 0 = 0 <=> H(a) = 0
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Intégrale pourquoi F(x) borné de x à a doit s'annuler e
zygomatique a écrit:salut
MDR (je suis désolé mais vu ton discours je ne peux m'en empécher ...)
Aha on est bien d'accord, mais "messieurs ne nous fâchons pas"
Borne sup, maths spé !
Re: Intégrale pourquoi F(x) borné de x à a doit s'annuler e
mais non zygomatique tu peux te marrer autant que tu veux, je t'ai dit qu'il ne s'agissait pas du double-bornage en a, tu sais lire? J'evoque uniquement la partie a et non x meme si celle-ci prenait la valeur de a, tu as un fichier joint qui te le montre avec a=0, j'peux pas mieux faire
Re: Intégrale pourquoi F(x) borné de x à a doit s'annuler e
écoute, avant de donner des leçon il faudrai déjà savoir de quoi on parle, vu tes explications ca n'a pas l'air d'être ton cas.
On cherche a montrer que \mathrm{d}x) est l'unique primitive de
est l'unique primitive de ) sur
sur  qui s'annule en
qui s'annule en 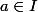 .
.
 = \int_{a}^a f(x) \mathrm{d}x = 0) car les deux bornes sont égales (convention).
car les deux bornes sont égales (convention).
Donc s'annule bien en
s'annule bien en 
Soit une primitive de
une primitive de  s'annulant en
s'annulant en  .
.
 et
et  étant deux primitives de
étant deux primitives de  ,
,  = F(x) + k)
Ainsi = F(a) + k = 0 + k = k) , or
, or  = 0) , donc
, donc 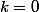 .
.
Ainsi, = F(x)) donc
donc 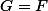 .
.
Donc est unique.
est unique.
Et ta proposition est démontrée. Si tu ne peux pas comprendre ca, on ne peut rien pour toi.
On cherche a montrer que
Donc
Soit
Ainsi
Ainsi,
Donc
Et ta proposition est démontrée. Si tu ne peux pas comprendre ca, on ne peut rien pour toi.
Borne sup, maths spé !
Re: Intégrale pourquoi F(x) borné de x à a doit s'annuler e
t'as effectivement rien compris tu penses qu'il s'agit de la règle banal d'avoir le même bornage en haut et en bas; quand on dit qu'elle s'annule en a dans le cadre de la primitive F(x) borné x et a, on évoque la deuxième partie de calcul de la primitive c'est-à-dire a, dans l'exemple tu as en deuxième partie de calcul 0^2+0(=0) si tu changes la primitive et que tu lui rajoutes une constante(ex:+1) tu auras en deuxième partie de calcul(donc en a!) 0^2+0+1=1, là en l'occurence la deuxième partie de calcul ne s'annule pas en a; (contenu supprimé par la modération) Il y a donc une exigence particulière à ce qu'elle s'annule en deuxième partie de calcul sinon cette règle sera valable pour f(x)= F(b)-F(a)(peu importe si les constantes s'annulent) dans l'intégralité du calcul
Modifié en dernier par Lostounet le 13 Jan 2017, 02:09, modifié 2 fois.
Raison: Insultes
Raison: Insultes
Re: Intégrale pourquoi F(x) borné de x à a doit s'annuler e
Bonsoir,
Quand on vient poser une question sur un forum et qu'une personne prend le temps de nous répondre, la moindre des choses (et des politesses) est de la remercier, non? Même si la réponse apportée ne te convient pas. Il est donc inacceptable d'insulter des personnes qui ont accepté de t'aider !
Merci donc de ne pas continuer dans l'agressivité... (qui a envie de se prendre la tête à répondre pour finalement se faire insulter?)
Pour répondre à ta question (bon je tente quand même):
En fait si on change de primitive, je reprends = 2t + 1)
Une primitive de f est bien entendu: = t^2 + t) Mais une autre pourrait aussi être
Mais une autre pourrait aussi être  = t^2 + t + 1) ou bien
ou bien  = t^2 + t + \pi) .
.
Par contre quelle que soit la primitive que tu choisis (G, K, ou encore H), la valeur numérique de l'intégraledt}) suivante ne change pas, puisqu'en effet:
suivante ne change pas, puisqu'en effet:
1) Si je choisis la primitive = t^2 + t + 1)
dt}) = H(a) - H(b) = a^2 + a + 1 - (b^2 + b + 1)
= H(a) - H(b) = a^2 + a + 1 - (b^2 + b + 1)

On constate que les constantes +1 et -1 s'annulent ! donc la valeur est a^2 + a - b^2 - b
2) Si je choisis la primitive = t^2 + t + \pi)
[/b]dt}) = K(a) - K(b)
= K(a) - K(b)
)

Puisqu'en effet +pi et -pi se simplifient !
Donc quelle que soit la primitive que tu choisis, les constantes ne jouent pas et la valeur de l'intégrale reste la même. Bien sûr que K(a) sera différent de G(a) ou de K(a) mais puisqu'on soustrait ensuiteK(a) de K(x) par exemple, les constantes se simplifient:
F(x) = K(x) - K(a) = x^2 + x + pi - a^2 - a - pi
C'est pour cela qu'il vaut mieux distinguer intégrale et primitive même si c'est très lié(en fait c'est au cœur de ta question!). Ce n'est pas un reproche contre toi, mais c'est à cause du fait que certaines fonctions n'admettent pas de primitive usuelle, et pourtant nous avons besoin de donner une valeur numérique à l'aire sous la courbe par exemple qui est [/b]dt})
Tu peux en fait interpréter F comme l'aire sous la courbe de la fonction f entre le point a et le point x. F(a) = K(a) - K(a) = G(a) - G(a) = H(a) - H(a)
Si je n'ai pas répondu à ta question... inutile de m'insulter: tu peux demander des précisions, ou reformuler ta question autrement.
Quand on vient poser une question sur un forum et qu'une personne prend le temps de nous répondre, la moindre des choses (et des politesses) est de la remercier, non? Même si la réponse apportée ne te convient pas. Il est donc inacceptable d'insulter des personnes qui ont accepté de t'aider !
Merci donc de ne pas continuer dans l'agressivité... (qui a envie de se prendre la tête à répondre pour finalement se faire insulter?)
Pour répondre à ta question (bon je tente quand même):
si tu changes la primitive et que tu lui rajoutes une constante(ex:+1) tu auras en deuxième partie de calcul(donc en a!) 0^2+0+1=1
En fait si on change de primitive, je reprends
Une primitive de f est bien entendu:
Par contre quelle que soit la primitive que tu choisis (G, K, ou encore H), la valeur numérique de l'intégrale
1) Si je choisis la primitive
On constate que les constantes +1 et -1 s'annulent ! donc la valeur est a^2 + a - b^2 - b
2) Si je choisis la primitive
[/b]
Puisqu'en effet +pi et -pi se simplifient !
Donc quelle que soit la primitive que tu choisis, les constantes ne jouent pas et la valeur de l'intégrale reste la même. Bien sûr que K(a) sera différent de G(a) ou de K(a) mais puisqu'on soustrait ensuiteK(a) de K(x) par exemple, les constantes se simplifient:
F(x) = K(x) - K(a) = x^2 + x + pi - a^2 - a - pi
C'est pour cela qu'il vaut mieux distinguer intégrale et primitive même si c'est très lié(en fait c'est au cœur de ta question!). Ce n'est pas un reproche contre toi, mais c'est à cause du fait que certaines fonctions n'admettent pas de primitive usuelle, et pourtant nous avons besoin de donner une valeur numérique à l'aire sous la courbe par exemple qui est [/b]
Tu peux en fait interpréter F comme l'aire sous la courbe de la fonction f entre le point a et le point x. F(a) = K(a) - K(a) = G(a) - G(a) = H(a) - H(a)
Si je n'ai pas répondu à ta question... inutile de m'insulter: tu peux demander des précisions, ou reformuler ta question autrement.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Intégrale pourquoi F(x) borné de x à a doit s'annuler e
t'as presque compris ma question, tu m'as énuméré l'annulation des constantes dans les calcul de l'intégrale et donc ma question de base est pourquoi une règle impose une annulation en a(deuxième partie de calcul je reprécise), tu m'expliques aussi conceptuellement ce qu'est une intégrale(aire en dessous de la courbe) , j'ai pas besoin de cela; si on utilise la primitive F(x) avec la variable x et un bornage en a et qu'il existe donc une unique primitive s'annulant en a(donc la preuve que cela concerne la deuxième partie de calcul sinon on pourrait sortir plusieurs primitives avec chacune leur constante s'annulant comme tu l'as décrit hors là il s'agit d'une annulation en a, il s'agit de l'exigence d'une règle concernant le bornage minimal appelé a autres exemple bidon :
x>a avec a=1 F(x)=In(x) s'annule en a pas parceque je remplace a par x mais parceque la simple deuxième partie de calcul =0 puisque In(1)=0 , c'est pour cela que dans l'exemple du haut il est t'es présenté le calcul expréssément sans que l'on est remplacé x, ce qui donnerait là F(x)= In(x)-In(1) et notre deuxième partie(a) est bien = à 0 , ma question est pourquoi cette règle exigente? Règle qui n'est pas imposé quand on calcul une intégrale normalement avec une fonction f(x)>F(b)-F(a)
x>a avec a=1 F(x)=In(x) s'annule en a pas parceque je remplace a par x mais parceque la simple deuxième partie de calcul =0 puisque In(1)=0 , c'est pour cela que dans l'exemple du haut il est t'es présenté le calcul expréssément sans que l'on est remplacé x, ce qui donnerait là F(x)= In(x)-In(1) et notre deuxième partie(a) est bien = à 0 , ma question est pourquoi cette règle exigente? Règle qui n'est pas imposé quand on calcul une intégrale normalement avec une fonction f(x)>F(b)-F(a)
Re: Intégrale pourquoi F(x) borné de x à a doit s'annuler e
paroxystique33 a écrit:il s'agit de l'exigence d'une règle concernant le bornage minimal appelé a autres exemple bidon :
x>a avec a=1 F(x)=In(x) s'annule en a pas parceque je remplace a par x mais parceque la simple deuxième partie de calcul =0 puisque In(1)=0 , [...]
Règle qui n'est pas imposé quand on calcul une intégrale normalement avec une fonction f(x)>F(b)-F(a)
Ce n'est pas parce que a vaut 1 que F s'annule en a. On n'est pas obligé de prendre a un point en lequel ln(x) est nul. Par exemple si a = 200, et qu'on considère cette fonction:
Il n'y a pas d'exigence sur la "borne minimale": dès qu'une fonction f est continue sur un intervalle [a ; b] elle admet une primitive sur [a;b]. Tu peux choisir tout a qui te convient (bien entendu pourvu que la fonction est continue sur l'intervalle par exemple),
Si cela ne répond pas à ta question, c'est principalement lié au fait que je ne l'ai pas comprise. Et vu que cela fait quelques années que j'apprends les maths... ben je te dis qu'il faut vraiment (conseil!) que tu emploies des termes plus précis. Par exemple:
intégrale normalement avec une fonction f(x)>F(b)-F(a)
f(b)-f(a) , on ne demande pas à ce que la primitive s'annule en a, pourquoi cette exigence?
merci de m'épargner vos commentaires négatifs du type"tu confonds intégrale et primitives bla bla"
Le problème est que tu confonds vraiment intégrale et primitive et que c'est ta source d'incompréhension!
D'ailleurs regarde, tu écris des fois f(b) - f(a) et d'autres fois F(b) - F(a) alors que c'est pas du tout du tout la même chose. Et lorsque tu dis "pourquoi on n'impose pas que la primitive s'annule en a lorsque F(b) - F(a)", c'est simple: parce que ceci n'est pas une primitive mais la valeur de l'intégrale !
tu m'expliques aussi conceptuellement ce qu'est une intégrale(aire en dessous de la courbe) , j'ai pas besoin de cela;
Peut-être que c'est pas directement ta question, mais vu le mix de termes mathématiques dans tes posts, on ne sait pas ce qui est compris et ce qui ne l'est pas encore.
Bref, vu que tu débutes en intégration il vaut mieux ne pas faire d'amalgames ni de raccourcis.
Cela te permettra de mieux comprendre. Personne n'a dit que c'était simple ni évident, la théorie de l'intégration est quelque chose de très compliqué... mais si on fait trop d'approximations et de raccourcis (surtout lorsqu'on débute quelque chose) on ne peut absolument rien comprendre à quoi que ce soit (ni aux bases, ni à la théorie)
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Intégrale pourquoi F(x) borné de x à a doit s'annuler e
Salut
Il s'avère que la fonction en question telle qu'elle est définie dans le théorème s'annule en a.
C'est un fait, pas du tout une exigence.
Bref, posée telle quelle, pour moi, ta question a autant de sens que si tu demandait dans le théorème qui dit que (a-b)(a+b)=a²-b², pourquoi on a "pris comme règle" de mettre a²-b² plutôt que a² tout seul (qui serait plus simple) ?
La réponse est on ne peut plus évidente, c'est qu'avec a²-b², c'est effectivement vrai (i.e. c'est un théorème) alors qu'avec a² tout seul ça ne le serait pas.
Et là, ben c'est exactement pareil, ce que te dit ce théorème, c'est que si f est continue sur l'intervalle I, qu'on prend a dans I et qu'on pose F(x)=intégrale de a à x de ... alors F est l'unique primitive de f qui s'annule en a.
Et le "qui s'annule en a" n'a absolument rien à voir avec une quelconque "règle", c'est une des conclusion du théorème, c'est tout.
Pour te donner un dernier exemple, dans le théorème de géométrie qui dit que :
Si D est une droite et A un point alors il existe une unique droite D' parallèle à D qui passe par A.
Est-ce que tu as un tant soit peu l'impression que le "qui passe par A" de la fin de la phrase à quoi que ce soit à voir avec "une règle" qu'on aurait "choisi" ?
On exige rien du tout.paroxystique33 a écrit:...je voulais savoir pourquoi dans cette forme d'intégrale écrite à l'aide d'une primitive on exige que celle-ci s'annule en a...
Il s'avère que la fonction en question telle qu'elle est définie dans le théorème s'annule en a.
C'est un fait, pas du tout une exigence.
Alors, il y a un truc qui faudrait bien que tu comprenne, c'est que dans le fichier joint que tu as mis dans ton premier post, le truc en question, ce n'est absolument pas "une règle", c'est un théorème, c'est à dire un truc qui se démontre et que le fait que la fonction F(x)=intégrale de a à x de ... soit l'unique primitive qui s'annule en a, ce n'est absolument pas un quelconque "choix" qui a été fait de "prendre celle qui s'annule en a", mais c'est un résultat que l'on démontre (aisément).paroxystique33 a écrit:t'as presque compris ma question, tu m'as énuméré l'annulation des constantes dans les calcul de l'intégrale et donc ma question de base est pourquoi une règle impose une annulation en a(deuxième partie de calcul je reprécise), tu m'expliques aussi conceptuellement ce qu'est une intégrale(aire en dessous de la courbe) , j'ai pas besoin de cela; si on utilise la primitive F(x) avec la variable x et un bornage en a et qu'il existe donc une unique primitive s'annulant en a(donc la preuve que cela concerne la deuxième partie de calcul sinon on pourrait sortir plusieurs primitives avec chacune leur constante s'annulant comme tu l'as décrit hors là il s'agit d'une annulation en a, il s'agit de l'exigence d'une règle concernant le bornage minimal appelé a autres exemple bidon :
x>a avec a=1 F(x)=In(x) s'annule en a pas parceque je remplace a par x mais parceque la simple deuxième partie de calcul =0 puisque In(1)=0 , c'est pour cela que dans l'exemple du haut il est t'es présenté le calcul expréssément sans que l'on est remplacé x, ce qui donnerait là F(x)= In(x)-In(1) et notre deuxième partie(a) est bien = à 0 , ma question est pourquoi cette règle exigente? Règle qui n'est pas imposé quand on calcul une intégrale normalement avec une fonction f(x)>F(b)-F(a)
Bref, posée telle quelle, pour moi, ta question a autant de sens que si tu demandait dans le théorème qui dit que (a-b)(a+b)=a²-b², pourquoi on a "pris comme règle" de mettre a²-b² plutôt que a² tout seul (qui serait plus simple) ?
La réponse est on ne peut plus évidente, c'est qu'avec a²-b², c'est effectivement vrai (i.e. c'est un théorème) alors qu'avec a² tout seul ça ne le serait pas.
Et là, ben c'est exactement pareil, ce que te dit ce théorème, c'est que si f est continue sur l'intervalle I, qu'on prend a dans I et qu'on pose F(x)=intégrale de a à x de ... alors F est l'unique primitive de f qui s'annule en a.
Et le "qui s'annule en a" n'a absolument rien à voir avec une quelconque "règle", c'est une des conclusion du théorème, c'est tout.
Pour te donner un dernier exemple, dans le théorème de géométrie qui dit que :
Si D est une droite et A un point alors il existe une unique droite D' parallèle à D qui passe par A.
Est-ce que tu as un tant soit peu l'impression que le "qui passe par A" de la fin de la phrase à quoi que ce soit à voir avec "une règle" qu'on aurait "choisi" ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Intégrale pourquoi F(x) borné de x à a doit s'annuler e
Et pour bien expliquer la différence, le théorème dont tu parle ici, il dit que :paroxystique33 a écrit:...alors que dans le cas de f(b)-f(a) , on ne demande pas à ce que la primitive s'annule en a...
Si F est une quelconque des primitives de f sur l'intervalle [a,b] alors l'intégrale de a à b de f(t)dt = F(b)-F(a).
Et ce que dit en particulier ce théorème et qui est extrêmement important, c'est que, si F et G sont deux primitives de f sur [a,b] alors on a forcément F(b)-F(a)=G(b)-G(a) c'est à dire que lorsque l'on calcule une intégrale à l'aide de la formule donnée par le théorème ci dessus, le résultat ne dépend (heureusement) pas de la primitive choisie.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Intégrale pourquoi F(x) borné de x à a doit s'annuler e
Mais si messieurs, c'est une exigence ce théorème de l'analyse, s'il existe une unique primitive qui s'annule en a, il en existe pas une infinité même si l'intégralité du calcul reviendrait au même en rajoutant une constante ou même pas du tout, il y a une exigence à c'qu'en deuxième partie de calcul quand on utilise cette forme avec la variable x, on parte de zéro soit a=0 pourquoi cette exigence? Peut-etre parceque justement il y a une utilité à ça dans les études supérieures des intégrales et je le répète cela ne concerne pas la règle simple et banale et bien connu de l'annulation en double-bornage(a;a ou x=a;a), soyez pas stupide ils n'ont pas établi ce théorème pour dire deux fois la même chose...En l'occurence quand on parle d'annulation on ne parle pas de l'annulation qui serait quand x=a combien de fois faut-il le répéter à tous ces érudits? Donc effectivement quand on utilise l'écriture du calcul d'une intégrale en utilisant une fonction simple f(x) et qu'on atterrit à F(b)-F(a) , dans cette forme d'écriture de calcul des intégrales , ce théorème d'annulation en F(a) n'est pas imposée. Pour rappel: cette annulation concerne effectivement a et donc la deuxième partie de l'intégrale , mon fichier joint l'indique bien la fonction s'annule en a qui prend la valeur zéro(0^2+0=0), l'exemple laisse volontairement x sans prendre aucune valeur pour bien montrer que la variable n'est pas concernée directement par la règle(en d'autres terme il ne s'agit pas de la remplacer par a). Un monsieur me dit plus haut que je pourrai très bien avoir pour F(x)=In(x) a=200 oui effectivement donc pour que F(x) s'annule en a F(x)=In(x)-5,29 c'est super ça m'avance à quoi dans la compréhension du théorème?
Re: Intégrale pourquoi F(x) borné de x à a doit s'annuler e
Visiblement tu ne comprends rien du tout et tu ne veux rien comprendre et c'est vite devenu insupportable.
Pire, tu crois tout comprendre des bases alors qu'il te manque les trois-quart des notions de base: tu confonds fonction, primitive, et intégrale. Tu veux nous faire croire que ta question n'a rien à avoir avec le fait d'avoir deux bornes égales alors que c'est exactement ça: quand tu fais F(a) et que tu remplaces tous les x par a, cela donne la bête règle on ne peut plus banale. On est tous dans le supérieur depuis un moment donc s'il y avait une once de sens dans ce que tu dis, on te l'aurait fait savoir.
J'ai essayé (avec les autres) de comprendre ta question et de t'expliquer des choses que tu ne comprends visiblement pas mais tu ne veux pas écouter ni lire quoi que ce soit.
Je préfère fermer la discussion plutôt que de te voir traiter des gens de stupides, surtout Ben314 (qui enseigne dans le supérieur) dont tu n'égaleras jamais ni le niveau ni les connaissances en mathématiques.
Pire, tu crois tout comprendre des bases alors qu'il te manque les trois-quart des notions de base: tu confonds fonction, primitive, et intégrale. Tu veux nous faire croire que ta question n'a rien à avoir avec le fait d'avoir deux bornes égales alors que c'est exactement ça: quand tu fais F(a) et que tu remplaces tous les x par a, cela donne la bête règle on ne peut plus banale. On est tous dans le supérieur depuis un moment donc s'il y avait une once de sens dans ce que tu dis, on te l'aurait fait savoir.
J'ai essayé (avec les autres) de comprendre ta question et de t'expliquer des choses que tu ne comprends visiblement pas mais tu ne veux pas écouter ni lire quoi que ce soit.
Je préfère fermer la discussion plutôt que de te voir traiter des gens de stupides, surtout Ben314 (qui enseigne dans le supérieur) dont tu n'égaleras jamais ni le niveau ni les connaissances en mathématiques.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
