Intégral substition trigonométrique
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
ernif
- Membre Naturel
- Messages: 12
- Enregistré le: 31 Juil 2008, 06:12
-
 par ernif » 31 Juil 2008, 07:52
par ernif » 31 Juil 2008, 07:52
Je dois trouver cet intégral:
int(sqrt(36+x^2)/x, x)
Hors je parviens à me rendre à cette étape avant de bloquer et de ne plus savoir quoi faire:
6*(int((1+tan^2*x)*secx/tan, x))
int = intégral
sqrt = racine carrée
Quelqu'un peut m'aider?
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 31 Juil 2008, 08:13
par le_fabien » 31 Juil 2008, 08:13
Bonjour,
Pour

la fonction à integrer est de la forme

.
Si j'ai bien compris ton énoncé...
-
ernif
- Membre Naturel
- Messages: 12
- Enregistré le: 31 Juil 2008, 06:12
-
 par ernif » 31 Juil 2008, 08:18
par ernif » 31 Juil 2008, 08:18
finalement je msuis tromper je dois résoudre
6*(int((1+tan^2*x)*secx/tan, x))
Ça aurait été trop facile sinon :briques:
P.S. J'aimerais bien savoir comment transférer mes équations en image.
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 31 Juil 2008, 08:21
par le_fabien » 31 Juil 2008, 08:21
Une question:
c'est quoi " secx " ? :hein:
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 31 Juil 2008, 08:22
par _-Gaara-_ » 31 Juil 2008, 08:22
Salut,
pour la première intégrale plusieurs IPP feront l'affaire ;)
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 31 Juil 2008, 08:32
par _-Gaara-_ » 31 Juil 2008, 08:32
Il y a mieux , enfin je crois :
mettre en facteur x² en haut, il reste :

EDIT : non ça complique le truc en fait :we:
-
ernif
- Membre Naturel
- Messages: 12
- Enregistré le: 31 Juil 2008, 06:12
-
 par ernif » 31 Juil 2008, 08:36
par ernif » 31 Juil 2008, 08:36
secx = sécante de x : sec(x)
Je me rends là dans la résolution de ma première intégral en faisant une substition trigo:
6*(int((1+tan(x)^2)*sec(x)/tan(x), x))
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 31 Juil 2008, 08:43
par _-Gaara-_ » 31 Juil 2008, 08:43
Substitution trigonométrique = changement de variable ?
:briques:
-
ernif
- Membre Naturel
- Messages: 12
- Enregistré le: 31 Juil 2008, 06:12
-
 par ernif » 31 Juil 2008, 08:45
par ernif » 31 Juil 2008, 08:45
je nsuis pas sur de comprendre commen tu as fait pour réduire l'équation ainsi garaa...
^2)*sec(x)}{tan(x)}dx)
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 31 Juil 2008, 08:47
par _-Gaara-_ » 31 Juil 2008, 08:47
ernif a écrit:secx = sécante de x : sec(x)
Je me rends là dans la résolution de ma première intégral en faisant une substition trigo:
6*(int((1+tan(x)^2)*sec(x)/tan(x), x))
Après avoir cherché on a bien : sec(x) = 1/cos(x)
donc
^2}{\cos(x) \tan(x)} = 6 \int \frac{1+\tan(x)^2}{\tan(x)} \times \fr{1}{\cos(x)})
maintenant IPP en posant : u(x) = 1/cos(x) et v'(x) = ce que LEFAB11 t'a dit
mais je suis curieux de savoir comment tu as procédé pour la "substitution" trigonométrique wahouuu :hein:
-
ernif
- Membre Naturel
- Messages: 12
- Enregistré le: 31 Juil 2008, 06:12
-
 par ernif » 31 Juil 2008, 08:47
par ernif » 31 Juil 2008, 08:47
oui on pose la variable
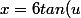)
pour ainsi enlever la racine carrée
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 31 Juil 2008, 08:52
par _-Gaara-_ » 31 Juil 2008, 08:52
ernif a écrit:je nsuis pas sur de comprendre commen tu as fait pour réduire l'équation ainsi garaa...
Tu as pour x différent de (SUB)Zero ^^
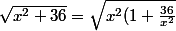} = x\sqrt{( 1 + \frac{36}{x^2} )})
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 31 Juil 2008, 08:53
par _-Gaara-_ » 31 Juil 2008, 08:53
ernif a écrit:oui on pose la variable
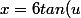)
pour ainsi enlever la racine carrée
Peux tu s'il te plaît m'en dire plus ?
comment tu as fait pour savoir qu'il fallait faire ça ? O_O
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 31 Juil 2008, 08:58
par rene38 » 31 Juil 2008, 08:58
Bonjour
_-Gaara-_ a écrit:Tu as pour x différent de (SUB)Zero ^^

Attention :

-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 31 Juil 2008, 09:02
par _-Gaara-_ » 31 Juil 2008, 09:02
rene38 a écrit:BonjourAttention :

oui j'oublie toujours XD :ptdr:
-
ernif
- Membre Naturel
- Messages: 12
- Enregistré le: 31 Juil 2008, 06:12
-
 par ernif » 31 Juil 2008, 09:02
par ernif » 31 Juil 2008, 09:02
_-Gaara-_ a écrit:Peux tu s'il te plaît m'en dire plus ?
comment tu as fait pour savoir qu'il fallait faire ça ? O_O
En posant
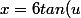)
nous avons:
^2}}{6tan(u)}*6sec(u)^2 dx)
d'où on peut mettre le 36 en évidance:
^2}}{6tan(u)}*6sec(u)^2 dx)
et ensuite:
^2}}{6tan(u)}*6sec(u)^2 dx)
pour enlever la racine:
^2}}{6tan(u)}*6sec(u)^2 dx = \int \frac{6sec(u)}{6tan(u)}*6sec(u)^2 dx)
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 31 Juil 2008, 09:10
par _-Gaara-_ » 31 Juil 2008, 09:10
Joli !!!! :doh: ****** c'est balaise !!
mais tu as fait intervenir un changement de variable >_<
là il te reste :
^3}{\tan(u)} du = 6\int \frac{\sec(u)\times \tan'(u)}{\tan(u)} du)
à ce stade c'est fini non ?
-
ernif
- Membre Naturel
- Messages: 12
- Enregistré le: 31 Juil 2008, 06:12
-
 par ernif » 31 Juil 2008, 09:22
par ernif » 31 Juil 2008, 09:22
_-Gaara-_ a écrit:Joli !!!! :doh: ****** c'est balaise !!
mais tu as fait intervenir un changement de variable >_<
là il te reste :
^3}{\tan(u)} du)
à ce stade c'est fini non ?
Non ce n'est pas fini il faut résoudre l'intégral et une fois résolu rechanger les variables en les plaçant dans un triangle rectable (L'hypothénuse serait

, le côté adjacent l'angle teta serait 6 et le côté opposé serait x, compte tenu que j'ai poser
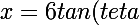.)
Maintenant je sais que ça donne:
}{tan(u)} dx + 6sec(u))
Quelqu'un sait ce que:
}{tan(u)} dx)
donne?
-
Black Jack
 par Black Jack » 31 Juil 2008, 09:26
par Black Jack » 31 Juil 2008, 09:26
Salut,
S'il s'agit bien de int(sqrt(36+x^2)/x, x), alors :
[racine(36+x²)]/x dx = [racine(36+x²)]/x² * x dx
Poser 36+x² = t²
x dx = t dt
x² = t²-36
[racine(36+x²)]/x dx = [t²/(t²-36)] dt
Et cela c'est classique ...
:zen:
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 31 Juil 2008, 09:28
par _-Gaara-_ » 31 Juil 2008, 09:28
Tu peux remarquer que :
sec(x) = tan(x)/sin(x)
l'intégrale que tu cherches deviens :
} du)
et sachant que : sin(u) = 2t/(1+t^2) avec t = tan(u/2)
tu devrais trouver
} du = \ln(\tan(\frac{u}{2})))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 98 invités


