[RESOLU] Injection - Surjection - bijection
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
kabakas
- Membre Naturel
- Messages: 74
- Enregistré le: 20 Jan 2013, 20:39
-
 par kabakas » 25 Oct 2015, 00:55
par kabakas » 25 Oct 2015, 00:55
salut à tous,
aidez-moi svp à résoudre cet exercice :
Cliquez sur l'image pour l'agrandir :

-
mathelot
 par mathelot » 25 Oct 2015, 11:12
par mathelot » 25 Oct 2015, 11:12
bjr,
i) utilise les lois de Boole (ou de Morgan (Morgan, c'est avec les complémentaires), je sais jamais)
 = (A \cup B ) \cap ( A \cup C))
 = (A \cap B ) \cup ( A \cap C))
ii) La définition d'une application injective est
=F(Y_2) \Rightarrow Y_1=Y_2) (*)
(*)iii) il peut t être utile de calculer les images pour certains cas particuliers, notamment:
,F(B),F(E),F(A \cup B),F(A\cap B), F(\emptyset))
, etc..
iv) tu peux dessiner des patatoïdes pour illustrer tes cogitations.
v) D'après (*) , si besoin de démontrer
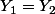
et que F est injective
=F(Y_2))
est une condition suffisante de
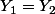
-
kabakas
- Membre Naturel
- Messages: 74
- Enregistré le: 20 Jan 2013, 20:39
-
 par kabakas » 25 Oct 2015, 11:59
par kabakas » 25 Oct 2015, 11:59
mathelot a écrit:bjr,
i) utilise les lois de Boole (ou de Morgan (Morgan, c'est avec les complémentaires), je sais jamais)
 = (A \cup B ) \cap ( A \cup C))
 = (A \cap B ) \cup ( A \cap C))
ii) La définition d'une application injective est
=F(Y_2) \Rightarrow Y_1=Y_2) (*)
(*)iii) il peut t être utile de calculer les images pour certains cas particuliers, notamment:
,F(B),F(E),F(A \cup B),F(A\cap B), F(\emptyset))
, etc..
iv) tu peux dessiner des patatoïdes pour illustrer tes cogitations.
v) D'après (*) , si besoin de démontrer
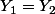
et que F est injective
=F(Y_2))
est une condition suffisante de
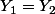
salut !
merci à vous de me répondre aussi vite.
mais j'ai rien compris !
où sont les réponses ???
-
mathelot
 par mathelot » 25 Oct 2015, 12:03
par mathelot » 25 Oct 2015, 12:03
kabakas a écrit:salut !
merci à vous de me répondre aussi vite.
mais j'ai rien compris !
où sont les réponses ???
hi,hi,hi :we:
Les réponses ne sont pas fournies.
C'est simplement une liste de propriétés qui peut être utile pour démontrer.
-
kabakas
- Membre Naturel
- Messages: 74
- Enregistré le: 20 Jan 2013, 20:39
-
 par kabakas » 25 Oct 2015, 12:06
par kabakas » 25 Oct 2015, 12:06
-
mathelot
 par mathelot » 25 Oct 2015, 12:08
par mathelot » 25 Oct 2015, 12:08
je te réécris mon post sans le français:
si
)
et
,)
alors
 = (A \cup B ) \cap ( A \cup C))
 = (A \cap B ) \cup ( A \cap C))
ii) La définition d'une application injective est
si
)
et
,)
alors
=F(Y_2) \Rightarrow Y_1=Y_2 (*))
iii) il peut t être utile de calculer les images suivantes:
,F(B),F(E),F(A \cup B),F(A\cap B), F(\emptyset))
, etc..
iv) tu peux faire des dessins pour t'aider.. v) D'après (*) , si besoin de démontrer
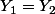
et si F est injective
=F(Y_2))
entraine
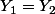
__________________
-
mathelot
 par mathelot » 25 Oct 2015, 12:11
par mathelot » 25 Oct 2015, 12:11
Ecris moi ce que tu as déjà fait et n'hésite pas à poser des questions.
-
mathelot
 par mathelot » 25 Oct 2015, 12:20
par mathelot » 25 Oct 2015, 12:20
QUestion 1.
Supposons

. Ecrivons la propriété pour f d' 'être injective.
-
kabakas
- Membre Naturel
- Messages: 74
- Enregistré le: 20 Jan 2013, 20:39
-
 par kabakas » 25 Oct 2015, 13:26
par kabakas » 25 Oct 2015, 13:26
mathelot a écrit:QUestion 1.
Supposons

. Ecrivons la propriété pour f d' 'être injective.

-
mathelot
 par mathelot » 25 Oct 2015, 13:29
par mathelot » 25 Oct 2015, 13:29
c'est parfait.
-
kabakas
- Membre Naturel
- Messages: 74
- Enregistré le: 20 Jan 2013, 20:39
-
 par kabakas » 25 Oct 2015, 13:55
par kabakas » 25 Oct 2015, 13:55
mathelot a écrit:c'est parfait.
Mais je suis coincé pour les autres.
-
kabakas
- Membre Naturel
- Messages: 74
- Enregistré le: 20 Jan 2013, 20:39
-
 par kabakas » 25 Oct 2015, 14:19
par kabakas » 25 Oct 2015, 14:19
mathelot a écrit:c'est parfait.
J'ai tenté ceci pour la surjection.

-
mathelot
 par mathelot » 25 Oct 2015, 15:07
par mathelot » 25 Oct 2015, 15:07
supposons

Montrons que F est surjective:
Soient
)
et
)
Posons

 \cup (A \cap B_0 )=A_0 \cup \emptyset = A_0)
de même

donc

est un antécédent de
.)
F est surjective.
-
mathelot
 par mathelot » 25 Oct 2015, 18:58
par mathelot » 25 Oct 2015, 18:58
on vient de montrer que

surjective
On va montrer que si

alors f n'est pas surjective.
Soit
=\{ \omega \}; \emptyset)


donc X n'existe pas, le couple
)
n'a pas d'antécédent et f n'est pas surjective.
-
mathelot
 par mathelot » 25 Oct 2015, 19:14
par mathelot » 25 Oct 2015, 19:14
pour comprendre le post de 19h58
considérer



A0={1,2,3} B0={4,5} , on voit que l'antécédent X doit à la fois contenir 3 et ne pas le contenir.
en généralisantSI (
_{i \in I})
est une partition de E
alors on a une bijection entre
)
et
)
-
kabakas
- Membre Naturel
- Messages: 74
- Enregistré le: 20 Jan 2013, 20:39
-
 par kabakas » 25 Oct 2015, 22:19
par kabakas » 25 Oct 2015, 22:19
mathelot a écrit:pour comprendre le post de 19h58
considérer



A0={1,2,3} B0={4,5} , on voit que l'antécédent X doit à la fois contenir 3 et ne pas le contenir.
en généralisantSI (
_{i \in I})
est une partition de E
alors on a une bijection entre
)
et
)
Merci.
Et la dernière ?
-
mathelot
 par mathelot » 26 Oct 2015, 09:16
par mathelot » 26 Oct 2015, 09:16
kabakas a écrit:Merci.
Et la dernière ?
c'est la question que je voulais te poser

On connaît l'image

et

.
L'application réciproque de F, G doit pouvoir reconstituer X à partir d'une image
)
A quelle condition sur A et B est ce possible ?
-
kabakas
- Membre Naturel
- Messages: 74
- Enregistré le: 20 Jan 2013, 20:39
-
 par kabakas » 26 Oct 2015, 13:59
par kabakas » 26 Oct 2015, 13:59
mathelot a écrit:c'est la question que je voulais te poser

On connaît l'image

et

.
L'application réciproque de F, G doit pouvoir reconstituer X à partir d'une image
)
A quelle condition sur A et B est ce possible ?
A C X et B C X
-
mathelot
 par mathelot » 26 Oct 2015, 17:13
par mathelot » 26 Oct 2015, 17:13
-
kabakas
- Membre Naturel
- Messages: 74
- Enregistré le: 20 Jan 2013, 20:39
-
 par kabakas » 28 Oct 2015, 13:26
par kabakas » 28 Oct 2015, 13:26
merci infiniment...
je passe en "Résolu"
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités

(*)
, etc..
et que F est injective
est une condition suffisante de