Inéquations difficiles

[pierrelouisbourgeois]

Bonjour,

Pouvez-vous m'aider à résoudre ces deux inéquations? Je suis en seconde et j'ai du mal avec les inéquations. Merci

[img]file:///C:/Users/Pilou/Pictures/Screenshots/Capture%20d%E2%80%99%C3%A9cran%20(3).png[/img]

[Sylviel]

L'image est sur ton disque dur et ne peut donc pas être vu sur le web. Il faut la mettre sur un site d'hébergement d'image, ou mieux, recopier l'énoncé.

[pierrelouisbourgeois]

Désolé, je n'y avais pas pensé.

3-x/x+4 >0

2x-1/x+3 > 2x/x-4

[infernaleur]

Salut,
si tu ne met pas de parenthèses, pour la première équation on lit :...
Mais bon je pense que toi c'est plutôt

Quand tu as un quotient ou un produit ( A/B ou A*B ) tu dois savoir que le signe dépend seulement des signes de A et de B. Par exemple 3/5 le signe sera positif car 3 est positif et 5 est positif, de même -2/3 sera négatif car -2 est négatif et 3 est positif.

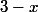Donc dans ton cas pour trouver le signe de , ce que tu dois faire c'est tout d'abord chercher le signe du numérateur et le signe du dénominateur .
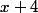Et une fois que tu aura fait ça tu résume tout dans un joli tableau de signe pour en déduire le signe de la fraction .



ATTENTION: on a une fraction donc on a pas le droit de diviser par 0 !!!! Donc avant de commencer la résolution on doit d'abord déterminer le domaine où la fonction est définie.

[WillyCagnes]

bonjour
(3-x)/(x+4)>0
on pose la condition du denominateur x<>-4

3-x >0 soit x<3
x+4 >0 soit x>-4

soit 3 > x >-4

[pierrelouisbourgeois]

Donc dans ton cas pour trouver le signe de , ce que tu dois faire c'est tout d'abord chercher le signe du numérateur et le signe du dénominateur .
Et une fois que tu aura fait ça tu résume tout dans un joli tableau de signe pour en déduire le signe de la fraction .



ATTENTION: on a une fraction donc on a pas le droit de diviser par 0 !!!! Donc avant de commencer la résolution on doit d'abord déterminer le domaine où la fonction est définie.

Mais le signe ne dépend-t-il pas de la valeur de x ? Cela peut varier...

[laetidom]

Bonsoir,

Mais le signe ne dépend-t-il pas de la valeur de x ? Oui

Cela peut varier... mais sur un intervalle de x défini dans le tableau de signes, le signe est constant

[pierrelouisbourgeois]

Ok, j'ai fait un tableau de signe pour la première inéquation. Quand est-il de la seconde svp?

[Sylviel]

Tu te ramènes à une seule inéquation puis tu fais un tableau de signe.

[pierrelouisbourgeois]

Merci.