Inéquation
21 messages
- Page 1 sur 2 - 1, 2
Inéquation
Voila, je me retrouve bloqué sur une inéquation et je ne vois pas comment continuer:
( Le V signifie racine carré):
V(x² - x + 20) > x
Apres avoir trouvé le domaine de l'inéquation : D = ]- infini ; -4 [ U ]5 ; +infini[
je ne sais plus quoi faire pour continuer...
( Le V signifie racine carré):
V(x² - x + 20) > x
Apres avoir trouvé le domaine de l'inéquation : D = ]- infini ; -4 [ U ]5 ; +infini[
je ne sais plus quoi faire pour continuer...
hé bien on étudie les solutions suivant le membre qui n'est pas sous la racine : "x"
Tu peux rédiger comme cela :
Si xx[/TEX] est vérifiée pour car tu aura toujours sous la racine quelque chose de positif et de négatif au membre de droite, Donc
car tu aura toujours sous la racine quelque chose de positif et de négatif au membre de droite, Donc 
Ensuite, tu traites le cas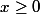 en élévant au carré.
en élévant au carré.
C'est un peu comme résoudre une équation de la forme où on veut que
où on veut que  or dans une inéquation, on envisage les deux cas :
or dans une inéquation, on envisage les deux cas : 
Tu peux rédiger comme cela :
Si xx[/TEX] est vérifiée pour
Ensuite, tu traites le cas
C'est un peu comme résoudre une équation de la forme
Salut !
Je suis conscient que tout ceci échappe un peu à ta compréhension, je vais donc synthétiser un peu tout ça pour que tout sois plus clair pour toi :++:
On veut résoudre :
1°) Cette inéquation est définie si et seulement si :

Pour cela on résous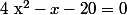 ,
, 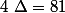 ,
,  donc
donc 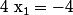 ou
ou 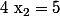 .
.
Or d'après le cours sur le signe du trinôme du second degré, le coefficient des termes en x² étant strictment positif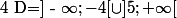 .
.
2°) Ensuite, on étudie le signe du deuxième membre de l'inéquation ( )
)
- Si xx[/TEX] est toujours vrai car et
et  , c'est-à-dire,
, c'est-à-dire,  , alors quelque soit x, on peut donc élever au carré :
, alors quelque soit x, on peut donc élever au carré :


Donc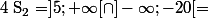
3°) En conclusion :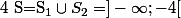
C'est bon là ?
Je suis conscient que tout ceci échappe un peu à ta compréhension, je vais donc synthétiser un peu tout ça pour que tout sois plus clair pour toi :++:
On veut résoudre :
1°) Cette inéquation est définie si et seulement si :
Pour cela on résous
Or d'après le cours sur le signe du trinôme du second degré, le coefficient des termes en x² étant strictment positif
2°) Ensuite, on étudie le signe du deuxième membre de l'inéquation (
- Si xx[/TEX] est toujours vrai car
Donc
3°) En conclusion :
C'est bon là ?
21 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
