Inéquation quotient

[Mat1313]

Bonjour à tous les matheux,
J'ai un souci avec une inéquation quotient.

Je dois résoudre

(x+4) / (5-x) strictement inférieur à 2

J'ai donc cherché des valeurs de x:

x+4= 2
x= (-2)

5-x=2
x=3

Sauf que quand je les rentre dans la calculatrice, je ne parviens pas aux bons résultats. Je vous remercie.
Mat

[Robic]

Houlà, tu mélanges tout ! :marteau:

L'inéquation est :


La technique habituelle (c'est-à-dire hors astuce) consiste à tout mettre à gauche et à mettre au même dénominateur :



Ensuite, on regroupe tout en une seule fraction et on peut utiliser un tableau de signe.

[Mat1313]

Bonjour Robic,
Si je continue dans ton sens, j'ai en numérateur
x + 4 - 10 - 2x
ou bien

x + 4 - 10 + 2x ?

Je vous tire un grand merci

[Fred_Sabonnères]

Bonjour
Il faut résoudre avec différent de

Si je multiplie par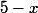 de part et d'autre de l'inégalité en supposant , je ne change pas le signe de l'inégalité.

Donc je dois résoudre
avec
avec
J'obtiens donc
avec
Donc les valeurs de vérifient l'inéquation

Mais ce n'ai pas fini car
si je multiplie par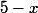 de part et d'autre de l'inégalité en supposant , je change le signe de l'inégalité.
je te laisse poursuivre :we:

[Mat1313]

Je ne comprends pas.

x + 4 < 10 - 2x Je suis d'accord

En revanche, on trouve 6/3 et non pas 7 / 3 si je ne m'abuse.

[Robic]

La méthode de Fred_Sabonnères est différente de celle que j'ai exposée et elle est plus risquée (quand on n'est pas trop à l'aise) car il faut distinguer deux cas (5-x>0, 5-x<0). Je pense que Mat1313 a intérêt à ne pas se disperser.

Si je continue dans ton sens, j'ai en numérateur
x + 4 - 10 - 2x
ou bien
x + 4 - 10 + 2x ?

Oui, c'est le deuxième ! Voici le détail :




Après avoir simplifié x+ 4 - 10 + 2x, il reste à utiliser un tableau de signe pour conclure.

[Fred_Sabonnères]

C'est vrai Robic que ta méthode est plus "standard" :ptdr:

[Mat1313]

Donc j'ai 3x = 6
x = 2

[Mat1313]

Ok, j'ai saisi:

S = (Moins l'infini;2(U)5; plus l'infini(

[Fred_Sabonnères]

Donc j'ai 3x = 6
x = 2

Ton inéquation se réduit à:



Tu dois donc faire un tableau de signe....

[Fred_Sabonnères]

Ok, j'ai saisi:

S = (Moins l'infini;2(U)5; plus l'infini(

C'est ça !!!! :we: :we: :we:

[Mat1313]

Merci beaucoup !
Comme quoi, la politesse amène toujours à la bonne entente.

[Robic]

Tu dis ça parce que j'ai oublié de te dire bonjour ? :salut:

Ta question était clairement posée, c'est aussi ça qui a aidé à obtenir de l'aide. (Parfois, on voit des questions sans réponse, on ne se demande pas pourquoi...)

[Mat1313]

Non, ce n'était pas ironique, rassurez-vous.

Une dernière question pour vous embêter ce soir:

x2-4x+3 < 0

Je factorise en:

(x-3)(x-1) < 0

Je trouve pour (x-3):
x-3 < 0
x<3

Et pour (x-1):

x-1<0
x<1
Alors qu'on devrait mieux avoir x>1, non ?

[Robic]

Avec (x-3)(x-1) < 0, là encore on peut faire un tableau de signe. Car pour qu'un produit soit négatif, on doit avoir des facteurs de signes contraires.

Donc il y a deux possibilités :
* soit x-3 négatif et x-1 positif,
* soit x-3 positif et x-1 négatif.

Mais si les deux sont négatifs, le produit sera positif (à cause de la règle des signes).