bonjour,bonsoir, bonne nuit!
j'ai quelques problèmes de méthode :cry:
eh bien voilà j'ai deux inéquations à résoudre dans R les voici:
(x²-2x+1)^3 <= 1
et
(x²-2x+1)² <= 1
donc je suppose qu'il est possible de les résoudre brutalement avec une chtite dérivation, une étude de signe et un tableau de variation puis enfin les racines évidentes 0 et 2
et paf ça ferait des chocapics!
mais je voudrais en fait savoir si j'ai le droit de procéder comme suit:
(x²-2x+1)^3 <= 1
<-> racine cubique((x²-2x+1)^3 ) <= racine cubique(1)
où la seule racine cubique de 1 réelle est 1
<-> (x²-2x+1) <= 1
<-> (x-1)² <= 1
<-> sqrt[(x-1)²] <= sqrt(1)
où les deux racines sont -1 et 1
en traitant ensuite les cas suivant
d'une part
-1 <= (x-1)
<-> x >= 0
d'autre part
(x-1) <= 1
<-> x <=2
et d'appliquer un raisonnement similaire à la seconde (avec deux passages aux racines carrées) car le passage aux racines me dérange assez...
en espérant avoir une réponse
Inéquation (méthode)
2 messages
- Page 1 sur 1
Bonsoir,
Ton raisonnement est bon.
Pour des nombres positifs, le passage aux racines dans les inégalités n'est pas dangereux, les fonctions "racines" étant strictement croissantes.
Evidemment, le danger est d'oublier que .
.
NB Personnellement, pour la deuxième, j'éviterais ces tracas en transposant le 1 et en utilisant un tableau de signes après avoir factorisé.
Pour la première tu peux essayer avec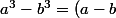(a^2+ab+b^2)) , mais cela risque de s'alourdir...
, mais cela risque de s'alourdir...
Ton raisonnement est bon.
nahel a écrit:et d'appliquer un raisonnement similaire à la seconde (avec deux passages aux racines carrées) car le passage aux racines me dérange assez...
Pour des nombres positifs, le passage aux racines dans les inégalités n'est pas dangereux, les fonctions "racines" étant strictement croissantes.
Evidemment, le danger est d'oublier que
NB Personnellement, pour la deuxième, j'éviterais ces tracas en transposant le 1 et en utilisant un tableau de signes après avoir factorisé.
Pour la première tu peux essayer avec
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
