Inéquation avec racine carré (factorisation)

[arnaud710]

Bonjour comment factoriser (x/4) -3 - ;)3 -2;)5 pour l'inéquation (x/4) -3 ;) x;)3 + 2;)5 ?
Merci d'avances.
ps : je suis en 2nde.

[uztop]

Salut,
la racine carrée est un nombre aussi. Il faut juste faire comme d'habitude ici: mettre tous les termes en x à gauche et tous les termes constants à droite

[arnaud710]

Salut,
la racine carrée est un nombre aussi. Il faut juste faire comme d'habitude ici: mettre tous les termes en x à gauche et tous les termes constants à droite

(x/4) -3 x;)3 + 2;)5
Donc (x/4) -x;)3 3 + 2;)5
(x-4x;)3)/4 3 + 2;)5
x-4x;)3 12 + 8;)5
Est ce juste ? Et après , que dos je faire ?

[uztop]

oui, on peut donc écrire
(1-4;)3) x ;) 12 + 8;)5
Il suffit maintenant de diviser pour trouver x ;) ...

[arnaud710]

oui, on peut donc écrire
(1-4;)3) x 12 + 8;)5
Il suffit maintenant de diviser pour trouver x ...

(x/4) -3 x;)3 + 2;)5
Je trouve x (48;)3 + 4;)15)/48.

Mais ma prof m'avait dit de faire un tableau de signes.

[uztop]

pour cette équation, il n'y a pas besoin de tableau de signes. Sauf si'il y a une erreur d'énoncé
Ca donne tout simplement

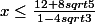
[arnaud710]

pour cette équation, il n'y a pas besoin de tableau de signes. Sauf si'il y a une erreur d'énoncé
Ca donne tout simplement

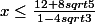
Donc la solution est ](moins l'infini) ; ... ] ?

[uztop]

oui, c'est très moche mais c'est bien ça...

[arnaud710]

oui, c'est très moche mais c'est bien ça...

Ma prof m'a dit de mettre les réponses dans des intervalles...