Inéquation avec paramètre

par **Dinozzo13** » 31 Oct 2009, 18:05

Bonjour, je me suis proposé de résoudre, l'inéquation définie avec paramètre par :

,

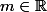
Voici ce que je trouve :
- si

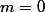
alors

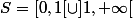
- si

alors

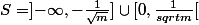
-{1}.
Ai-je bon ?

par **Ericovitchi** » 31 Oct 2009, 18:17

pour m= 0 d'accord
mais pour m<0 je ne comprends pas. Ton expression est du signe de x(mx²-1) donc du signe de -x puisque le second facteur est toujours négatif.
donc quand x est négatif, l'expression est positive
seuls les x positifs sont à garder

Et pour le dernier c'est OK

par **Dinozzo13** » 31 Oct 2009, 18:30

ok, je vais donc regarder plus attentivement le cas m<0, merci Ericovitchi ^^.

par **Black Jack** » 31 Oct 2009, 18:30

Je suis d'accord avec la remarque de Ericovitchi pour le cas m 0

La partie de l'ensemble notée [0 , 1/Vm[ - {1} est litigieuse.

a) parce que "1" ne fait pas partie de [0 , 1/Vm[ si m est > 1, et donc on ne peut pas retirer {1} d'un ensemble dans lequel il ne figure pas obligatoirement.

b) il n'y a pas de raison pour que le [0 , 1/Vm[ soit ouvert du coté 1/Vm

Si on veut éviter toute ambiguité, il faudrait séparer le cas m > 0 en 2 cas différents.
0 1

:zen:

par **Dinozzo13** » 31 Oct 2009, 18:49

ok, je tiendrai compte de ça dans mon raisonnement ^^.

Inéquation avec paramètre

inéquation avec paramètre

Qui est en ligne