Inégalités
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 19 Juil 2014, 20:59
par Sake » 19 Juil 2014, 20:59
Hello hello,
Comme je suis en train de me remettre aux inégalités (Titou(an ?) m'ayant donné envie), je propose de créer ce topic pour recenser tous les exos que les forumeurs voudraient partager ou dont ils voudraient avoir une solution, en rapport avec les inégalités. Tous niveaux confondus, je poste ce sujet dans la partie lycée car on ne rencontre pas seulement des inégalités dans les olympiades, et qui plus est, ces concours sont de niveau lycée.
Une question élémentaire tout d'abord.
Quelqu'un aurait une méthode par Cauchy-Schwarz pour montrer que
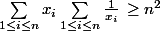
? Il y a une méthode toute indiquée par IAG (les xi sont positifs strictement bien sûr), et je suis en train de chercher une méthode par réordonnement/Chebyshev. Seulement par C-S, je tombe sur
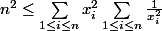
Me suis-je trompé qqpart ?
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 19 Juil 2014, 21:39
par jlb » 19 Juil 2014, 21:39
Une question élémentaire tout d'abord.
Quelqu'un aurait une méthode par Cauchy-Schwarz pour montrer que
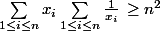
?
Ben, par Cauchy Schwartz!!! avec xi = (racine(xi))² et 1/xi=(1/racine(xi))²

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 19 Juil 2014, 21:50
par Sake » 19 Juil 2014, 21:50
jlb a écrit:Une question élémentaire tout d'abord.
Quelqu'un aurait une méthode par Cauchy-Schwarz pour montrer que
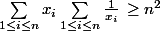
?
Ben, par Cauchy Schwartz!!!
Haha merci pour ton aide !
Sérieusement, je voulais dire le raisonnement, quoi. En plus s'il le faut cette méthode marche pas.
En fait si elle marche, en considérant les racines pour coordonnées des deux vecteurs. Fausse alerte :triste:
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 19 Juil 2014, 21:52
par jlb » 19 Juil 2014, 21:52
Sake a écrit:Haha merci pour ton aide !
Sérieusement, je voulais dire le raisonnement, quoi. En plus s'il le faut cette méthode marche pas
xi est positif? xi= (racine(xi))² et 1/xi=(1/racine(xi))² et Cauchy Schwartz ensuite

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 20 Juil 2014, 07:29
par zygomatique » 20 Juil 2014, 07:29
salut
on peut remarquer aussi que la fonction inverse est convexe donc :
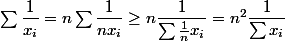
....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
t.itou29
- Membre Rationnel
- Messages: 601
- Enregistré le: 22 Jan 2013, 16:20
-
 par t.itou29 » 20 Juil 2014, 09:17
par t.itou29 » 20 Juil 2014, 09:17
J'ai un problème que je me suis posé il y a pas longtemps qui fait intervenir les inégalités :
Quel est le triangle inscrit dans le cercle unité dont le produit des côtés est maximal ? (et le prouver)
J'ai trouvé une solution mais je me demande s'il n'y pas plus simple.
Sinon pour l'inégalité précédente avec Chebyshev c'est direct car on peut supposer x-{i} croissant et donc 1/-x-{i} décroissant.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 20 Juil 2014, 10:47
par zygomatique » 20 Juil 2014, 10:47
t.itou29 a écrit:Sinon pour l'inégalité précédente avec Chebyshev c'est direct car on peut supposer x-{i} croissant et donc 1/-x-{i} décroissant.
en notant m et M le minimum et le maximum des x_i
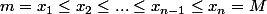
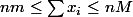
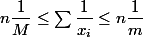
donc

j'aimerais bien voir ta preuve ....
autre méthode ::
la fonction f(x) = x + 1/x admet le minimum 2 en 1
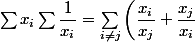 + \sum \dfrac {x_i}{x_i} \ge 2\dfrac {n^2 - n}{2} + n = n^2)
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
t.itou29
- Membre Rationnel
- Messages: 601
- Enregistré le: 22 Jan 2013, 16:20
-
 par t.itou29 » 20 Juil 2014, 10:53
par t.itou29 » 20 Juil 2014, 10:53
zygomatique a écrit:en notant m et M le minimum et le maximum des x_i
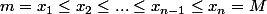
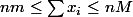
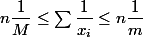
donc

j'aimerais bien voir ta preuve ....
autre méthode ::
la fonction f(x) = x + 1/x admet le minimum 2 en 1
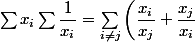 + \sum \dfrac {x_i}{x_i} \ge 2\dfrac {n^2 - n}{2} + n = n^2)
x-{i} et 1\x-{i} sont monotones de sens contraires, donc d'après l'inégalité de Chebyshev:
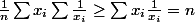
D'où l'inégalité si je ne me suis pas trompé
C'est pas mal aussi avec le minimum de x+1\x, il y a tellement de méthodes !

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 20 Juil 2014, 11:06
par zygomatique » 20 Juil 2014, 11:06
merci ... je ne connaissais pas cette relation ...
en gros la moyenne des produits est supérieure ou inférieure au produit des moyenne suivant la même monotonie ou non des deux suites ...
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 20 Juil 2014, 11:20
par Sake » 20 Juil 2014, 11:20
zygomatique a écrit:merci ... je ne connaissais pas cette relation ...
en gros la moyenne des produits est supérieure ou inférieure au produit des moyenne suivant la même monotonie ou non des deux suites ...
:lol3:
En gros oui. C'est issu de l'inégalité du réordonnement : Parmi toutes les permutations que l'on peut effectuer sur la famille des (y_i), seule celle où les y_i sont classés dans l'ordre croissant (les x_i aussi rangés dans le même ordre) fera que la somme des x_i*y_i sera maximale. Elle est minimale pour la permutation qui au i-ème élément des y_i fera correspondre y_(n-i)
-
t.itou29
- Membre Rationnel
- Messages: 601
- Enregistré le: 22 Jan 2013, 16:20
-
 par t.itou29 » 20 Juil 2014, 20:54
par t.itou29 » 20 Juil 2014, 20:54
Bonsoir,
J'aimerais avoir de l'aide pour finir ce problème:
Soit
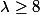
et
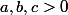
, montrer que:
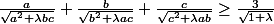
J'ai trouvé ceci:
Si on suppose convexe la fonction suivante:
=\frac{x}{\sqrt{x^2+\frac{\lambda abc}{x}}}=\frac{1}{\sqrt{1+\frac{\lambda abc}{x^3}})
En utilisant l'inégalité de Jensen et I.A.G on peut montrer l'inégalité.
Mon problème est purement calculatoire, pour montrer que f est convexe je dois calculer sa dérivée seconde, avec wolfram alpha je trouve bien une expression positive (qui explique d'ailleurs le lambda>=8) mais impossible de la retrouver à la main. Je dois tomber sur ça:
http://www.wolframalpha.com/input/?i=second+derivative+%281%2Ba%2Fx%5E3%29%5E%28-1%2F2%29 mais j'arrive à
u'^2+uu''])
(avec n=-1/2 et u=1+lambda*abc/x^3) et quand je remplace ça me donne un truc assez moche. :mur:
Je me demande si j'ai choisi la bonne fonction ...
Pourtant une fois qu'on a montré que la fonction est convexe le reste marche bien

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 20 Juil 2014, 21:42
par Sake » 20 Juil 2014, 21:42
t.itou29 a écrit:Bonsoir,
J'aimerais avoir de l'aide pour finir ce problème:
Soit
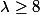
et
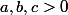
, montrer que:
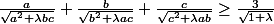
J'ai trouvé ceci:
Si on suppose convexe la fonction suivante:
=\frac{x}{\sqrt{x^2+\frac{\lambda abc}{x}}}=\frac{1}{\sqrt{1+\frac{\lambda abc}{x^3}})
En utilisant l'inégalité de Jensen et I.A.G on peut montrer l'inégalité.
Mon problème est purement calculatoire, pour montrer que f est convexe je dois calculer sa dérivée seconde, avec wolfram alpha je trouve bien une expression positive (qui explique d'ailleurs le lambda>=8) mais impossible de la retrouver à la main. Je dois tomber sur ça:
http://www.wolframalpha.com/input/?i=second+derivative+%281%2Ba%2Fx%5E3%29%5E%28-1%2F2%29 mais j'arrive à
u'^2+uu''])
(avec n=-1/2 et u=1+lambda*abc/x^3) et quand je remplace ça me donne un truc assez moche. :mur:
Je me demande si j'ai choisi la bonne fonction ...
Pourtant une fois qu'on a montré que la fonction est convexe le reste marche bien
Un truc assez moche qui a de fortes chances d'être correct. Suffit maintenant de réarranger ça pour obtenir la même formule que wolfram.
-
t.itou29
- Membre Rationnel
- Messages: 601
- Enregistré le: 22 Jan 2013, 16:20
-
 par t.itou29 » 20 Juil 2014, 21:49
par t.itou29 » 20 Juil 2014, 21:49
Sake a écrit:Un truc assez moche qui a de fortes chances d'être correct. Suffit maintenant de réarranger ça pour obtenir la même formule que wolfram.
Oui je crois que j'ai pas le choix...
Je ferai ça demain matin, à cette heure je peux plus réfléchir :ptdr:

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 20 Juil 2014, 22:26
par Sake » 20 Juil 2014, 22:26

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 20 Juil 2014, 22:36
par zygomatique » 20 Juil 2014, 22:36
et comment on fait pour lire ça ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 20 Juil 2014, 22:42
par Sake » 20 Juil 2014, 22:42
Tu copies le latex, tu le colles sur ta zone de texte, tu enlèves le \color{white} et puis "aperçu".
Pour le reste, change juste la couleur.
Enjoy :zen:

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 20 Juil 2014, 23:03
par fatal_error » 20 Juil 2014, 23:03
et comment on fait pour lire ça ?
firebug+highlight le contenu + attribut html:
style="background-color:black;" :lol3:
la vie est une fête


-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 20 Juil 2014, 23:24
par Sake » 20 Juil 2014, 23:24
Haha tu es un petit plaisantin ! Sauf si Zygomatiques a des connaissances en html, oui...
(psst, comment je fais ça sur chrome ?)

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 20 Juil 2014, 23:33
par zygomatique » 20 Juil 2014, 23:33
salut
une idée qui peut simplifier grandement les calculs ... ce me semble-t-il ...
posons
 = \dfrac{a}{\sqrt{a^2 + tbc}} + \dfrac{b}{\sqrt{b^2 + tca}} + \dfrac{c}{\sqrt{c^2 + tab}})
alors f est invariante par permutation du triplet (a, b, c)
de plus pour tout réel k > 0 :: f(a, b, c) = f(ka, kb, kc)
donc quitte à permuter a, b et c on peut supposer 0 < a =< b =< c et en multipliant alors le triplet par 1/a on en déduit que
 = f(1, b, c) = \dfrac{1}{\sqrt{1 + tbc}} + \dfrac{b}{\sqrt{b^2 + tc}} + \dfrac{c}{\sqrt{c^2 + tb}})
avec 1 =< b =< c
to be continued .... :lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 20 Juil 2014, 23:34
par zygomatique » 20 Juil 2014, 23:34
fatal_error a écrit:firebug+highlight le contenu + attribut html:
style="background-color:black;" :lol3:
no comprendo ...

Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
