Inégalités
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
t.itou29
- Membre Rationnel
- Messages: 601
- Enregistré le: 22 Jan 2013, 16:20
-
 par t.itou29 » 20 Juil 2014, 23:45
par t.itou29 » 20 Juil 2014, 23:45
Je viens de rendre compte que ce que j'ai fait est faux... Je sais pas pourquoi mais je me suis persuadé que abc>=x^3 et donc que la dérivée seconde est positive mais en prenant par exemple x=max{a;b;c} c'est complément faux ! Toute ma preuve est donc fausse ...
Désolé de t'avoir fait faire ce calcul fastidieux pour rien (au moins je t'ai occupé ta soirée :ptdr: )
Du coup j'ai regardé la solution et il fallait remarquer que l'inégalité était homogène et qu'on peut donc supposer a+b+c=1, puis utiliser a,b,c comme "poids" dans l'inégalité de Jensen appliquée à la fonction 1/sqrt(x) qui est beaucoup plus simple a dériver pour montrer la convexité !
Je me précipite tout le temps et me rend compte à la fin que c'est faux :mur:

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 21 Juil 2014, 08:45
par Sake » 21 Juil 2014, 08:45
Ben c'est pareil pour moi tu sais :D
-
t.itou29
- Membre Rationnel
- Messages: 601
- Enregistré le: 22 Jan 2013, 16:20
-
 par t.itou29 » 24 Juil 2014, 18:30
par t.itou29 » 24 Juil 2014, 18:30
Bonsoir,
J'ai de nouveau besoin d'aide, pour résoudre un problème j'aurais besoin de montrer que:
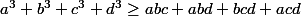
Et j'aimerais savoir si c'est correct :
En supposant a>=b>=c>=d, alors d'après l'inégalité du réordonnement (2 fois):

Et
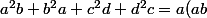+b(ab)+c(cd)+d(cd)\ge abc+abd+cda+cdb)
J'ai du me tromper car 'je dois montrer que A>=max{B;C} (où A,B,C sont 3 expressions dépendant de a,b,c,d) et si ce que j'ai fait est bon alors ça prouve que A>=B et A>=C. En soi c'est pas un problème mais alors je vois pas l'intérêt du max...
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 24 Juil 2014, 21:59
par Mikihisa » 24 Juil 2014, 21:59
Tu peux pas nous en dire un peu plus sur A B et C ? Parceque la comme ça :/
-
t.itou29
- Membre Rationnel
- Messages: 601
- Enregistré le: 22 Jan 2013, 16:20
-
 par t.itou29 » 24 Juil 2014, 22:05
par t.itou29 » 24 Juil 2014, 22:05
Mikihisa a écrit:Tu peux pas nous en dire un peu plus sur A B et C ? Parceque la comme ça :/
L'inégalité à prouver est :
)
avec
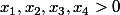
tels que
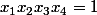
Comme x^3 est convexe on peut montrer que:
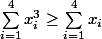
Et si ce que j'ai écrit dans mon premier message est correct on aurait aussi:

Ce qui me pousse à croire que je me suis trompé quelque part...
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 24 Juil 2014, 23:06
par Mikihisa » 24 Juil 2014, 23:06
Bah dire que [(a>b) et (a>c)] est équivalent a dire que a>max(b,c), donc je pense qu'on se prend la tête pour rien au final ^^
-
t.itou29
- Membre Rationnel
- Messages: 601
- Enregistré le: 22 Jan 2013, 16:20
-
 par t.itou29 » 25 Juil 2014, 07:57
par t.itou29 » 25 Juil 2014, 07:57
Mikihisa a écrit:Bah dire que [(a>b) et (a>c)] est équivalent a dire que a>max(b,c), donc je pense qu'on se prend la tête pour rien au final ^^
Oui ! je suis vraiment bête là dessus (pour pas dire autre chose...)
Dans le cas d'un minimum ça aurait été différent mais je sais pas pourquoi j'ai fait un bloquage sur le maximum. Ceux qui ont fait l'énoncé voulaient juste gagner de la place en évitant le " [(a>b) et (a>c)] " :ptdr:
Et au fait, est-ce que c'est bon la démonstration avec le réordonnement ?
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 25 Juil 2014, 09:15
par Mikihisa » 25 Juil 2014, 09:15
Bah ça me semble correct en effet tu utilise la permutation b a d c puis c d a b.
-
qelmcpc
- Membre Naturel
- Messages: 72
- Enregistré le: 07 Avr 2014, 18:23
-
 par qelmcpc » 26 Juil 2014, 10:06
par qelmcpc » 26 Juil 2014, 10:06
Salut,
J'ai une inégalité à démontrer par récurrence (donc pas de cauchy-schwarz, IAG ou je ne sais quoi)
La voici :
^2}{ \bigsum_{i=1}^{n} b_i})
Voilà, merci beaucoup!
-
qelmcpc
- Membre Naturel
- Messages: 72
- Enregistré le: 07 Avr 2014, 18:23
-
 par qelmcpc » 26 Juil 2014, 12:25
par qelmcpc » 26 Juil 2014, 12:25
Ah non, c'est bon, j'ai trouvé.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
et
