Inégalité
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
mathlegend
- Membre Relatif
- Messages: 133
- Enregistré le: 13 Nov 2010, 17:40
-
 par mathlegend » 20 Nov 2010, 13:44
par mathlegend » 20 Nov 2010, 13:44
bonjour a tous
soit x.y de (R) tel que (x+y=1)
prouver que (1+1/x^n)(1+1/y^n) >= (1+2^n)² (n = nombre naturel)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 20 Nov 2010, 13:52
par Ben314 » 20 Nov 2010, 13:52
A mon avis, il faut que x et y soient positifs : essaye avec n=3 et x=-1...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
mathlegend
- Membre Relatif
- Messages: 133
- Enregistré le: 13 Nov 2010, 17:40
-
 par mathlegend » 20 Nov 2010, 13:58
par mathlegend » 20 Nov 2010, 13:58
oui . x et y sont positifs pardon

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 20 Nov 2010, 14:03
par Ben314 » 20 Nov 2010, 14:03
Dans ce cas, l'étude de
=(1+x^{-n})(1+y^{-n}))
où

sur ]0,1[ permet de conclure.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
mathlegend
- Membre Relatif
- Messages: 133
- Enregistré le: 13 Nov 2010, 17:40
-
 par mathlegend » 20 Nov 2010, 16:24
par mathlegend » 20 Nov 2010, 16:24
merci gentilhomme :lol3:
-
mathlegend
- Membre Relatif
- Messages: 133
- Enregistré le: 13 Nov 2010, 17:40
-
 par mathlegend » 20 Nov 2010, 16:26
par mathlegend » 20 Nov 2010, 16:26
je vaudrais une autre résolution sans léetude de fonction si ca ne te dérange pas

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 20 Nov 2010, 20:00
par Olympus » 20 Nov 2010, 20:00
Salut !
J'ai une solution n'utilisant que AM-GM d'ordre 2 et la récurrence . Je la posterai dès que j'aurais un peu de temps ( là je suis occupé par un gros DM de chimie ... ) .
-
mathlegend
- Membre Relatif
- Messages: 133
- Enregistré le: 13 Nov 2010, 17:40
-
 par mathlegend » 20 Nov 2010, 20:06
par mathlegend » 20 Nov 2010, 20:06
oui je t'attends olympus et bonne chance avec ton DM

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 20 Nov 2010, 20:13
par Olympus » 20 Nov 2010, 20:13
Bon allez f*** la chimie :marteau: , voici ma solution :
 \left( 1+ \frac{1}{y^n} \right) = \left( 1+ \left( 1 + \frac{y}{x}\right)^n \right) \left( 1+ \left( 1+ \frac{x}{y}\right)^n \right) = \left( 1+ \frac{x}{y}\right)^n + \left( 1+ \frac{y}{x}\right)^n + 1 + \left( \left( 1+ \frac{x}{y}\right)\left( 1+ \frac{y}{x}\right) \right)^n)
Par AM-GM :
\left( 1+ \frac{y}{x}\right) \right)^n \geq 2^{2n})
.
Il nous suffira donc de prouver que
^n + \left( 1+ \frac{x}{y} \right)^n \geq 2^{n+1})
.
Pour

c'est évident . On supposera que c'est vrai pour un
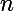
quelconque .
On a
 - \left( 1 + \frac{x}{y} \right) \right) \left( \left( 1+\frac{y}{x}\right)^n - \left( 1 + \frac{x}{y} \right)^n \right) \geq 0)
^{n+1} + \left( 1+\frac{x}{y} \right)^{n+1} \geq \left( 1+\frac{x}{y} \right) \left( 1+\frac{y}{x}\right)^n + \left( 1+\frac{y}{x}\right) \left( 1+\frac{x}{y} \right)^n)
On ajoute ensuite
^{n+1} + \left( 1+\frac{x}{y} \right)^{n+1})
aux deux côtés :
^{n+1} + \left(1+\frac{x}{y} \right)^{n+1} \geq \frac{1}{2} \left( 2+\frac{x}{y} + \frac{y}{x} \right) \left( \left(1+\frac{y}{x}\right)^n + \left( 1+\frac{x}{y}\right)^n \right) \geq 2^{n+2})
Par récurrence blabla ... CQFD
-
mathlegend
- Membre Relatif
- Messages: 133
- Enregistré le: 13 Nov 2010, 17:40
-
 par mathlegend » 20 Nov 2010, 20:19
par mathlegend » 20 Nov 2010, 20:19
trés bien meme si je ne sait pas que veut dire AM-GM

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 20 Nov 2010, 20:22
par Olympus » 20 Nov 2010, 20:22
mathlegend a écrit:trés bien meme si je ne sait pas que veut dire AM-GM
AM-GM d'ordre 2 ce n'est autre que l'inégalité
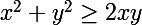
:lol3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 82 invités
