Inégalité du réordonnement

[t.itou29]

Bonjour,
J'ai une inégalité à prouver:
pour
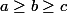
Je me demande si je ne peux pas utiliser l'inégalité du réordonnement mais je ne suis pas sûr de l'avoir très bien comprise. Si je suppose alors et .
Le produit des deux suites est donc minimal quand elles sont rangées dans l'ordre contraire, i.e:

Après il me suffirait d'enlever 3 à chaque terme et de montrer qu'ils sont positifs, est-ce correct ?
Merci

[Ericovitchi]

Bonsoir, oui pour moi ça tient la route.

Ensuite effectivement tu peux étudier la fonction f(x)=(x^3+2)/(x²-x+1) et montrer qu'elle est supérieure à 3 pour x>=1. C'est bien le cas :

[spike0789]

Bonjour,

Ou plus rapidement remarquer que :


Or pour , on a

Donc

[t.itou29]

Merci à vous deux ! Pour le (a+1)^3, j'y étais arrivé mais dans le sens inverse: en enlevant 3 et en factorisant après. Par contre je suis pas obligé de montrer que le dénominateur est positif c'est évident ?

[spike0789]

Positif ? Non. Mais non nul pour a dans R oui (cela revient au même je te l'accorde).
Discriminant négatif et on peut diviser

[chan79]

Salut
une autre approche en utilisant l'égalité ci-dessus, citée par spike0789:








les 3 quotients de gauche sont positifs et la grande parenthèse de droite est supérieure à 1
car cette moyenne arithmétique des 3 fractions est supérieure ou égale à leur moyenne géométrique qui est 1.
Finalement l'expression est supérieure ou égale à 9

[t.itou29]

Merci, c'est plus élégant ça évite d'avoir recours à l'analyse je pense que c'était la solution attendue. En fait c'est un exercice d'un site: awesomemath, tous les trois mois ils publient un set de problèmes. Celui là
était un junior mais ça va jusqu'à undergraduate et certains sont assez compliqués: je ne comprends même pas l'énoncé !