Inégalité à prouver par récurrence

[Aquillaa]

Bonjour,
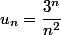
J'essaie de prouver par récurrence que la suite est supérieure ou égale à pour
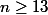
Pas de problème pour l'initialisation mais je bloque sur l'hérédité. Des idées ?
Merci d'avance

[lyceen95]

Je propose un autre exercice (le même en fait, mais présenté un peu différement) :

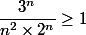
Prouver par récurrence que pour

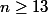
[Aquillaa]

C'est effectivement la même chose mais je bloque au même endroit. Pas moyen de retrouver l'hypothèse de récurrence quand je la considère vraie et que je passe à n+1.

[Aquillaa]

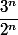
Ah ça y est je l'ai : il faut plutôt comparer avec [tex]n^2[tex]