Inégalité intégrale
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Ckronikks
- Membre Naturel
- Messages: 21
- Enregistré le: 25 Juil 2015, 10:41
-
 par Ckronikks » 25 Juil 2015, 11:02
par Ckronikks » 25 Juil 2015, 11:02
Bonjour je bloque sur une question alors si vous pouviez m'aider en me guidant ce serait sympa.
Les informations que j'ai jusqu'à maintenant:
-
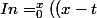^n*e^t/n!)dt)
-
!)+ I(n+1))
-
+(x^3/3!)+...+(x^n/n!))

Et voilà la question: Montrer que pour tout x R,
dt|<ou=\bigint_{a}^{b}|f(t)|dt)
. Attention au signe de x.
Merci d'avance :we:
-
Ckronikks
- Membre Naturel
- Messages: 21
- Enregistré le: 25 Juil 2015, 10:41
-
 par Ckronikks » 25 Juil 2015, 11:38
par Ckronikks » 25 Juil 2015, 11:38
Personne pour m'aider ? :hein:
-
Ckronikks
- Membre Naturel
- Messages: 21
- Enregistré le: 25 Juil 2015, 10:41
-
 par Ckronikks » 25 Juil 2015, 13:49
par Ckronikks » 25 Juil 2015, 13:49
Vraiment personne svp?
-
Ckronikks
- Membre Naturel
- Messages: 21
- Enregistré le: 25 Juil 2015, 10:41
-
 par Ckronikks » 25 Juil 2015, 15:20
par Ckronikks » 25 Juil 2015, 15:20
Une petite piste a me proposer ?

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 25 Juil 2015, 16:04
par Sake » 25 Juil 2015, 16:04
Bonjour,
Sans feuille ni crayon devant moi, Taylor-Lagrange pourra peut-être te donner quelque chose (?)
-
Ckronikks
- Membre Naturel
- Messages: 21
- Enregistré le: 25 Juil 2015, 10:41
-
 par Ckronikks » 25 Juil 2015, 16:22
par Ckronikks » 25 Juil 2015, 16:22
Oui, c'est Taylor Lagrange mais on ne l'a pas vu en terminale, donc je maitrise pas trop
-
Ckronikks
- Membre Naturel
- Messages: 21
- Enregistré le: 25 Juil 2015, 10:41
-
 par Ckronikks » 25 Juil 2015, 16:26
par Ckronikks » 25 Juil 2015, 16:26
Est ce que j'ai le droit d'écrire?: si x>0
^n*e^t/n!|dt= \bigint_{0}^{x}(x-t)^n*e^t/n!dt)

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 25 Juil 2015, 20:15
par zygomatique » 25 Juil 2015, 20:15
salut
supposons x > 0 ...

car la fonction
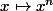
est croissante sur

supposons x 0 ....sauf que .... on n'oublie pas de ....
:ptdr:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Ckronikks
- Membre Naturel
- Messages: 21
- Enregistré le: 25 Juil 2015, 10:41
-
 par Ckronikks » 25 Juil 2015, 21:56
par Ckronikks » 25 Juil 2015, 21:56
Donc j'ai pour x> 0:

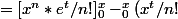'*e^t dt)

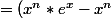/n!)
Et je fais pour x <0 donc ca met les valeurs absolues
C'est ça?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 25 Juil 2015, 22:34
par zygomatique » 25 Juil 2015, 22:34
:hein: :hein: :hein: :hein:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Ckronikks
- Membre Naturel
- Messages: 21
- Enregistré le: 25 Juil 2015, 10:41
-
 par Ckronikks » 25 Juil 2015, 22:38
par Ckronikks » 25 Juil 2015, 22:38
Bah j'ai fait une IPP.. ca marche pas ?
-
Ckronikks
- Membre Naturel
- Messages: 21
- Enregistré le: 25 Juil 2015, 10:41
-
 par Ckronikks » 26 Juil 2015, 00:31
par Ckronikks » 26 Juil 2015, 00:31
Sinon en moins chiant j'ai pour x> 0:


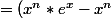/n!)
Et je fais après pour x <0
Ça marche comme ça ?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 26 Juil 2015, 10:32
par zygomatique » 26 Juil 2015, 10:32
en gros ... il suffit de lire ce que j'ai écrit ... et de le réfléchir ....
pourquoi développer ce x^n ? ....
exp est positive ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Ckronikks
- Membre Naturel
- Messages: 21
- Enregistré le: 25 Juil 2015, 10:41
-
 par Ckronikks » 26 Juil 2015, 10:34
par Ckronikks » 26 Juil 2015, 10:34
Mais quand est ce que j'ai développé le x^n?
-
Ckronikks
- Membre Naturel
- Messages: 21
- Enregistré le: 25 Juil 2015, 10:41
-
 par Ckronikks » 26 Juil 2015, 10:39
par Ckronikks » 26 Juil 2015, 10:39
Mais ça change rien que j'écrive
/n!)
ou
/n!)
nan?
-
Ckronikks
- Membre Naturel
- Messages: 21
- Enregistré le: 25 Juil 2015, 10:41
-
 par Ckronikks » 26 Juil 2015, 10:44
par Ckronikks » 26 Juil 2015, 10:44
Mais ce que je comprend pas c'est que si x>0: x^n>0 et (e^x-1)>0 et n!>0 donc le résultat est positif
Mais si x0 et (e^x-1)0 donc le résultat est négatif
Et pour n impair: x^n<0 et (e^x-1)<0 ... Donc positif

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 26 Juil 2015, 11:00
par zygomatique » 26 Juil 2015, 11:00
1/ il faut évidemment connaître les variations des fonctions x --> x^n en fonction de n ...
2/ il y a toujours le temps de développer si nécessaire ....
3/ exp(x) 1 suivant que x > 0 ou x < 0 ...
c'est pourquoi on majore |I_n| ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Ckronikks
- Membre Naturel
- Messages: 21
- Enregistré le: 25 Juil 2015, 10:41
-
 par Ckronikks » 26 Juil 2015, 11:11
par Ckronikks » 26 Juil 2015, 11:11
D'accord mais ça m'avance a quoi ?
Sinon je calcule tout en valeur absolue:
*e^t|dt=(|x|^n/n!)\bigint_{0}^{|x|}e^tdt)
Donc
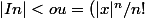*(e^{|x|}-1))

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 26 Juil 2015, 11:46
par zygomatique » 26 Juil 2015, 11:46
ça change à se simplifier la vie .... à aller à l'essentiel ... à écrire proprement les choses (de la façon la plus minimaliste possible mais avec toute l'exactitude exigée) ...
supposons x > 0 ...
)
car la fonction
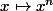
est croissante sur

supposons x 0 ....sauf que .... on n'oublie pas de ....
:ptdr:
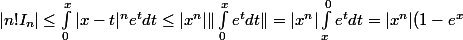)
donc dans tous les cas ::
|)
....
:zen:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Ckronikks
- Membre Naturel
- Messages: 21
- Enregistré le: 25 Juil 2015, 10:41
-
 par Ckronikks » 26 Juil 2015, 13:17
par Ckronikks » 26 Juil 2015, 13:17
Merci de ton aide

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités