Inégalité difficile

[Sara1999]

Bonjour, je ne sais pas comment répondre à cette question , pouvez-vous m’aider? Merci d’avance.
a, b, c et d 4 réels tels que a>=b>=c>=d et
a +b+c+d=9 et a^2+b^2+c^2+d^2=21,
Montrer que ab-cd >=2
J’ai ramené le problème à montrer que 9(a+b)-(a^2+b^2)-32>=0 mais pas plus.

[Mateo_13]

Bonjour,

je ne suis pas arrivé à résoudre le problème,
mais j'ai développé
et j'ai utilisé les deux hypothèses pour en déduire la valeur de ,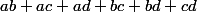
ensuite j'ai laissé intacts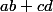 et dans les quatre autres termes,
j'en ai factorisé deux par a et deux autres par b, puis j'ai factorisé par ,
puis j'ai remplacé par ,
ce qui m'a fait apparaître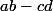 en fonction de et seuls, mais je n'ai pas pu continuer.

Désolé, amicalement,

[GaBuZoMeu]

Bonjour,

Le minimum de ab-cd est réalisé pour a=3, b=c=d=2.

Faute de mieux, on peut essayer les techniques bourrin de calcul différentiel : rechercher un point critique de ab-cd à l'intérieur du domaine ou en restriction aux bords du domaine, valeurs aux coins du domaine.

[Sara1999]

Bonjour,
Merci beaucoup pour vos propositions. Néanmoins, est ce que je peux savoir pourquoi le minimum de ab-cd et atteint lorsque à=3 et b=c=d=2?

[Black Jack]

Bonjour,

Approche à peaufiner :

a+b+c+d=9 et a^2+b^2+c^2+d^2=21,

(a+b+c+d=9)² = 9²
a²+b²+c²+d² + 2(ab+ac+ad+bc+bd+cd) = 81
21 + 2(ab+ac+ad+bc+bd+cd) = 81
ab+ac+ad+bc+bd+cd = 30
ab+cd + a(c+d)+b(c+d) = 30
ab+cd + (a+b).(c+d) = 30
ab+cd + (9-(c+d)).(c+d) = 30
ab+cd + (9c+9d-(c²+d²+2cd)) = 30
ab-cd + 9c+9d-c²-d² = 30
ab-cd = 30 - 9c - 9d + c² + d²
f(c,d) = 30 - 9c - 9d + c² + d²
df/dd = -9 + 2d (et comme d < V21, df/dd < 0 et f est décroissante avec d pour un c donné)
Et pareillement : f est décroissante avec c pour un d donné)

Ou si on préfère :
ab-cd = 30 - 9c - 9d + c² + d²
ab-cd = 30 - 9(9-a-b) + 21 - a² - b²
ab-cd = -30 + 9a + 9b - a² - b²
f(a,b) = -30 + 9a + 9b - a² - b²

Pour un b donné :
df/da = 9 - 2a
mais a² <= 21 et a >= 9/4 ---> 9/4 <= a <= V21
Donc df/da = 9 - 2a > 0 et f est croissante avec a sur sur tout l'intervalle possible de variation de a.
Il n'y a donc pas de max local à f(a,b)

Le max de (ab-cd) est pour la plus grande valeur de a possible qui permet que a+b+c+d=9 et a^2+b^2+c^2+d^2=21 soient respectés.

b^2+c^2+d^2 = 21-a² --> 21 - (V21)² <= b²+c²+d² <= 21 - (9/4)²
0 <= b²+c²+d² <= 255/16

Et comme a doit être le plus grand possible, il faut que b²+c²+d² soit le plus petit possible (en respectant les contraintes de départ)
... ce qui sera le cas pour b = c = d car ... à justifier.

On a donc
3b² + a² = 21
3b + a = 9

3*(9-a)²/9 + a² = 21
(9-a)² + 3a² = 63
4a² - 18a + 18 = 0
a = 1,5 ou 3 ... mais a = 1,5 est interdit puisque on doit avoir 9/4 <= a <= V21
--> a = 3 et b = c = d = (9-3)/3 = 2

[GaBuZoMeu]

Sara1999, peux-tu préciser le contexte de ta question : exercice scolaire ? quel niveau ? autre origine ?

[Sara1999]

Merci beaucoup Black, c’est vraiment loin d’être facile pour moi.
Pour répondre à GaBuZoMeu, je suis juste une passionnée d’inégalités depuis le lycée jusqu’aux classes prépas où je suis.

[Mateo_13]

Merci Black Jack pour la fin de la démonstration.

Si on revient à l'énoncé de départ,
le système des deux égalités ressemble à l'intersection d'une sphère et d'un hyperplan en dimension 4,
et en dimension 3, l'intersection d'une sphère et d'un plan serait un cercle.

Amicalement,

[GaBuZoMeu]

Bonjour,

J'explique comment utiliser le calcul diff pour minimiser (et maximiser)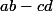 sur le domaine considéré, donné par les équations 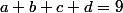et 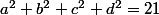(qui décrivent bien une 3-sphère) et les inégalités .

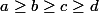J'utilise SageMath pour ne pas me fatiguer.

Code: Tout sélectionner

a,b,c,d=var("a,b,c,d")
P=a+b+c+d-9
Q=a^2+b^2+c^2+d^2-21
R=a*b-c*d

Le domaine a des coins où deux des inégalités sont des égalités. Cherchons ces coins, et les valeurs de R en ces coins.

Code: Tout sélectionner

Coin1=solve([P==0,Q==0,a==b,b==c],[a,b,c,d],solution_dict=True)
filtre = lambda s : s[a]>=s[b] and s[b] >= s[c] and s[c]>=s[d]
Coin1=list(filter(filtre,Coin1))
Coin1


[{a: 5/2, b: 5/2, c: 5/2, d: 3/2}]

Code: Tout sélectionner

ValCoin1=R.subs(Coin1)
ValCoin1

5/2

Code: Tout sélectionner

Coin2=solve([P==0,Q==0,a==b,c==d],[a,b,c,d],solution_dict=True)
Coin2=list(filter(filtre,Coin2))
Coin2

[{a: 1/4*sqrt(3) + 9/4,
b: 1/4*sqrt(3) + 9/4,
c: -1/4*sqrt(3) + 9/4,
d: -1/4*sqrt(3) + 9/4}]

Code: Tout sélectionner

ValCoin2=R.subs(Coin2)
expand(ValCoin2)

9/4*sqrt(3)

Code: Tout sélectionner

Coin3=solve([P==0,Q==0,b==c,c==d],[a,b,c,d],solution_dict=True)
Coin3=list(filter(filtre,Coin3))
Coin3

[{a: 3, b: 2, c: 2, d: 2}]

Code: Tout sélectionner

ValCoin3=R.subs(Coin3)
ValCoin3

2

Ceci fait, on cherche les points critiques de la restriction de R aux bords du domaine, où une des inégalités est une égalité. Et si la liste des points critiques n'est pas vide, les valeurs de R en ces points critiques.

Code: Tout sélectionner

# Bord1 : variables a,b,c, d=c
PB1=P.subs(d=c)
QB1=Q.subs(d=c)
RB1=R.subs(d=c)
J1=jacobian([PB1,QB1,RB1],[a,b,c])
CritB1=solve([J1.determinant()==0, P==0,Q==0, d==c],[a,b,c,d],
             domain='real',solution_dict=True)
filtreB1 =  lambda s : s[a]>s[b] and s[b] > s[c]
CritB1=list(filter(filtreB1,CritB1))
CritB1

[]

Code: Tout sélectionner

# Bord2 : variables a,b,d, c=b
PB2=P.subs(c=b)
QB2=Q.subs(c=b)
RB2=R.subs(c=b)
J2=jacobian([PB2,QB2,RB2],[a,b,d])
CritB2=solve([J2.determinant()==0, P==0,Q==0, c==b],[a,b,c,d],
             domain='real',solution_dict=True)
filtreB2 =  lambda s : s[a]>s[b] and s[c] > s[d]
CritB2=list(filter(filtreB2,CritB2))
CritB2

[{a: 2.77443798939126,
b: 2.327934413117377,
c: 2.327934413117377,
d: 1.569693094629156}]

Code: Tout sélectionner

ValCritB2=R.subs(CritB2)
ValCritB2

2.8045670995441743

Code: Tout sélectionner

# Bord3 : variables a,c,d, b=a
PB3=P.subs(b=a)
QB3=Q.subs(b=a)
RB3=R.subs(b=a)
J3=jacobian([PB3,QB3,RB3],[a,b,d])
CritB3=solve([J3.determinant()==0, P==0,Q==0, b==a],[a,b,c,d],
             domain='real',solution_dict=True)
filtreB3 =  lambda s : s[b]>s[c] and s[c] > s[d]
CritB3=list(filter(filtreB3,CritB3))
CritB3

[]

Et pour terminer, recherche des points critiques à l'intérieur du domaine où toutes les inégalités sont strictes, avec éventuellement valeurs de R en ces points critiques.

Code: Tout sélectionner

# Intérieur
J=jacobian([P,Q,R],[a,b,c,d])
Mins=[J.delete_columns([i]) for i in range(4)]
Crit=solve([M.determinant()==0 for M in Mins]+[P==0,Q==0],[a,b,c,d],
          domain='real',solution_dict=True)
filtreint = lambda s : s[a]>s[b] and s[b]>s[c] and s[c] > s[d]
Crit=list(filter(filtreint,Crit))
Crit

[]

Morale : minimum 2 atteint uniquement au coin {a: 3, b: 2, c: 2, d: 2} et maximum 9/4*sqrt(3) (à peu près 3.9) atteint uniquement au coin {a: 1/4*sqrt(3) + 9/4, b: 1/4*sqrt(3) + 9/4, c: -1/4*sqrt(3) + 9/4, d: -1/4*sqrt(3) + 9/4}.

[GaBuZoMeu]

Le max de (ab-cd) est pour la plus grande valeur de a possible qui permet que a+b+c+d=9 et a^2+b^2+c^2+d^2=21 soient respectés.

Je rappelle que l'exercice consiste à montrer que le MINIMUM de ab-cd sur le domaine considéré est supérieur ou égal à 2.