Bonjour,
Quelle est la limite en +∞ de : 4,6^x-1(ln(1-1/6^x) ?
Merci à par avance.
Indétermination 0/0
4 messages
- Page 1 sur 1
Re: Indétermination 0/0
Salut,
Je comprend pas grand chose
Si, comme tu l'écrit, ta limite c'est^x-\ln\big(1-\frac{1}{6^x}\big)) alors il y a zéro indétermination.
alors il y a zéro indétermination.
Je comprend pas grand chose
Si, comme tu l'écrit, ta limite c'est
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Indétermination 0/0
Bonjour Ben,
L'indétermination réside dans la formule de la limite en 0 de ln(1+x)/x qui sert à résoudre la limite en l'infini de 4,6^(x-1)*ln(1-1/6^x).
Le corrigé indique -2/3 comme réponse.
J'aurais aimé avoir le détail des calculs car je suis pas convaincu.
Merci de ton aide.
L'indétermination réside dans la formule de la limite en 0 de ln(1+x)/x qui sert à résoudre la limite en l'infini de 4,6^(x-1)*ln(1-1/6^x).
Le corrigé indique -2/3 comme réponse.
J'aurais aimé avoir le détail des calculs car je suis pas convaincu.
Merci de ton aide.
Re: Indétermination 0/0
Si, finalement ton truc c'est ça : 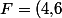^{x-1}\ln\big(1-\frac{1}{6^x}\big)) alors c'est pas du tout 2/3 la limite, mais 0 :
alors c'est pas du tout 2/3 la limite, mais 0 :
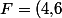^{x-1}\!\times\!\big(-\frac{1}{6^x}\big)\!\times\!\dfrac{\ln\big(1-\frac{1}{6^x}\big)}{-\frac{1}{6^x}}=-\dfrac{1}{4,\!6}\big(\frac{4,\!6}{6}\big)^{x}\!\times\!\dfrac{\ln\big(1-\frac{1}{6^x}\big)}{-\frac{1}{6^x}})
Le dernier terme c'est du}{t}) avec
avec  qui tend vers 0 donc ça tend vers 1 et, vu que
qui tend vers 0 donc ça tend vers 1 et, vu que  , à une puissance qui tend vers l'infini, ça tend vers 0.
, à une puissance qui tend vers l'infini, ça tend vers 0.
Le dernier terme c'est du
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
