Zebulon a écrit:Théorème :

dont la décomposition en produit de facteurs premiers est
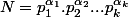
,
quel que soit D un diviseur de N, il existe

tels que
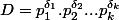
et

Preuve :
Soit
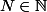
dont la décomposition en facteurs premiers est
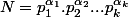
,
soit D un diviseur de N. Soit
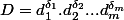
la décomposition de D en produit de puissances de facteurs premiers. Alors

.
On veut montrer que

(i).
\in\{1,2,...,k\},\ d_i=p_{j(i)})
et
(ii).
})
.
(i). Soit

,
D divise N et
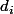
divise D, donc
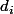
divise N. Comme
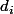
est premier,
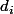
est un diviseur premier de N, donc
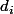
apparaît dans la décomposition de N en produit de puissnaces de facteurs premiers :

donc il existe
\in\{1,2,...,k\})
tel que
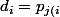})
.
On peut donc réécrire D :
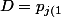}^{\delta_1}.p_{j(2)}^{\delta_2}...p_j(m)^{\delta_m}=p_{j(1)}^{\delta_1}.p_{j(2)}^{\delta_2}...p_j(m)^{\delta_m}.\prod\limits_{1\leq n\leq k}p_n^0=p_{j(1)}^{\delta_1}.p_{j(2)}^{\delta_2}...p_j(k)^{\delta_k})
avec
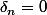
si
},p_{j(2)},...,p_{j(m)\})
.
(ii). Soit

,
supposons
})
, alors il existe
}\in\mathbb{N},\ r_{j(i)}>0,\ \delta_i=\alpha_{j(i)}+r_{j(i)})
et
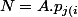}^{\delta_i-r_{j(i)}})
, avec
}^{r_{j(i)}})
qui ne divise pas A puisque A se décompose en produit de puissances de facteurs premiers, et que
})
n'apparaît pas dans cette décomposition.
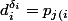}^{\delta_i})
divise N. Effectuons cette division :
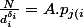}^{-r_{j(i)}}={A\over{p_{j(i)}^{r_{j(i)}}})
. Or
}^{r_{j(i)}})
ne divise pas A donc

n'est pas un entier et donc
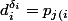}^{\delta_i})
ne divise pas N, ce qui est absurde.
Donc
})
.
Ca paraît compliqué car les notations sont lourdes, mais si on reprend l'exemple, on le voit bien (je rédige ça dans mon prochain message...)
