Incohérences des nombres décimaux

[Kugge]

Bonjour,
J'ai récemment lu un livre qui faisait le lien entre terminale et licence mathématiques, et il y avait écrit les affirmations suivantes :
(Partie développement décimaux)







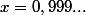
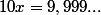
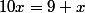
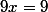
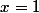
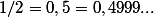
Juste après il y a marqué "On peut écrire rien qu'avec des 9 après le 4."
J'ai de gros doutes concernant ce raisonnement.. Il y a-t-il une incohérence ? Ou bien c'est juste vrai et admis ? Pourquoi ?

[Tuvasbien]

C’est vrai,0.9999 est l’écriture décimale impropre de 1, on peut aussi l’écrire

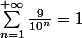
[Kugge]

C’est vrai,0.9999 est l’écriture décimale impropre de 1, on peut aussi l’écrire

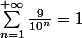
En effet, après avoir envoyé ma question j'ai encore cherché de mon côté et je suis tombé sur le résultat suivant justifiant cette affirmation :


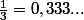
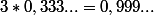
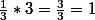
Or donc

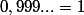
Merci pour votre réponse.

[Lostounet]

Bonjour,
J'ai récemment lu un livre qui faisait le lien entre terminale et licence mathématiques, et il y avait écrit les affirmations suivantes :
(Partie développement décimaux)







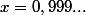
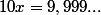
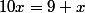
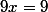
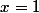
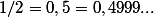
Juste après il y a marqué "On peut écrire rien qu'avec des 9 après le 4."
J'ai de gros doutes concernant ce raisonnement.. Il y a-t-il une incohérence ? Ou bien c'est juste vrai et admis ? Pourquoi ?

Salut,
Tu peux considérer la suite:

U(n+1)= U(n)/10 + 0.9
U(0)=0

Elle a pour formule explicite U(n)=1-10^(-n)
Et pour termes 0
0.9
0.99
0.999

Elle a pour limite 1

[mathelot]

C'est grâce à l'existence des développements décimaux impropres que l'ensemble des réels est connexe (d'un seul morceau,sans trou)