Impossible de comprendre ce calcul...
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Nane
- Membre Naturel
- Messages: 13
- Enregistré le: 04 Mai 2014, 22:20
-
 par Nane » 04 Mai 2014, 22:29
par Nane » 04 Mai 2014, 22:29
Bonjour a tous,
Je suis tombée sur une équations que je n'arrive pas à comprendre :triste: :
Il y a deux équations préliminaires:
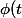 = \frac{f(t)}{S(t)} = - \frac{d ln(S(t))}{dt})
et,
 = 1 - \int_0^t f(u)du)
Partant de ces deux équations, ils donnent:
 = exp( - \int_0^t \phi(u)du ))
Les étapes de calcul intermédiaire ne sont pas données et je ne comprends pas comment ils arrivent à cette égalité... :mur:
Une idée?
Merci beaucoup,
Nane
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 04 Mai 2014, 23:48
par Sourire_banane » 04 Mai 2014, 23:48
Nane a écrit:Bonjour a tous,
Je suis tombée sur une équations que je n'arrive pas à comprendre :triste: :
Il y a deux équations préliminaires:
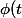 = \frac{f(t)}{S(t)} = - \frac{d ln(S(t))}{dt})
et,
 = 1 - \int_0^t f(u)du)
Partant de ces deux équations, ils donnent:
 = exp( - \int_0^t \phi(u)du ))
Les étapes de calcul intermédiaire ne sont pas données et je ne comprends pas comment ils arrivent à cette égalité... :mur:
Une idée?
Merci beaucoup,
Nane
Yop,
A partir de la première équation, tu as
=-\phi(t)\mathrm{d}t)
d'où, en intégrant :
)-\ln(S(0))=-\int_{0}^t \phi(u)\mathrm{d}u)
(parce que les variables sont muettes et que je suis physicien donc je m'en fiche)
Puisque S(0)=1, on a l'égalité.
-
Nane
- Membre Naturel
- Messages: 13
- Enregistré le: 04 Mai 2014, 22:20
-
 par Nane » 05 Mai 2014, 00:01
par Nane » 05 Mai 2014, 00:01
Ok ! :)
Merci 1000 fois!
nane
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 05 Mai 2014, 09:25
par paquito » 05 Mai 2014, 09:25
}{dt})
est la dérivée logarithmique de S(t), soit
}{S(t)})
et donc f(t)=-S'(t), ce qui justifie
=1-\bigint_{0}^{t}f(u)du)
. (Mais pour établir cette relation, on a besoin de S(0)=1, donc est que S(0)=1 est une hypothèse de l'énoncé? Sinon, ça pose un problème pour la dernière étape, sauf si cette relation est une donnée de l énoncé)
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 05 Mai 2014, 09:55
par Sourire_banane » 05 Mai 2014, 09:55
Il y a deux équations préliminaires
Paquito, c'est une donnée de l'énoncé donc il n'y a pas besoin de le démontrer !
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 05 Mai 2014, 14:17
par paquito » 05 Mai 2014, 14:17
Sourire_banane a écrit:Paquito, c'est une donnée de l'énoncé donc il n'y a pas besoin de le démontrer !
'
D'accord, merci; je ne savais pas si c'était une question.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
