[1èreS] DM : Hyperbole et droites
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Kso
- Membre Naturel
- Messages: 50
- Enregistré le: 02 Nov 2008, 16:54
-
 par Kso » 30 Oct 2009, 14:21
par Kso » 30 Oct 2009, 14:21
Bonjour,
J'ai un DM de maths assez difficile (on est sur le chapitre des polynômes au second degré) et j'ai vraiment besoin de votre aide. Merci d'avance, voilà l'énoncé :
Le but de l'exercice est d'étudier l'intersection d'une hyperbole et d'une droite variable .Soit f est la fonction définie par f(x) =

pour x différent de -1.
1) Trouver deux réels a et b tels que f(x) = a+
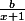
pour tout x différent de -1.
Voilà ce que j'ai fait :
f(x) =
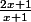
=

=
}{x+1})
-
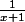
= 2 -
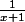
2) Par la méthode de votre choix, étudier le sens de variation de f sur ]-

;-1] puis sur ]-1;+ -

] . Dresser le tableau de variation de f.
Je suis bloquée ici, pourriez-vous m'aider ? Merci d'avance.
-
kushiki
- Membre Naturel
- Messages: 32
- Enregistré le: 21 Oct 2009, 14:40
-
 par kushiki » 30 Oct 2009, 15:23
par kushiki » 30 Oct 2009, 15:23
Bonjour,
tu fais f ' (x), tu étudies le signe de f ' sur l'intervalle demandé et tu as le sens de variations de f.
-
Kso
- Membre Naturel
- Messages: 50
- Enregistré le: 02 Nov 2008, 16:54
-
 par Kso » 30 Oct 2009, 15:46
par Kso » 30 Oct 2009, 15:46
Merci beaucoup, j'avais déjà pensé à la dérivée mais je ne sais pas comment passer de f(x) à f'(x). Comment fait-on ?
Merci d'avance.
-
jameso
- Membre Naturel
- Messages: 62
- Enregistré le: 11 Aoû 2006, 15:12
-
 par jameso » 30 Oct 2009, 16:05
par jameso » 30 Oct 2009, 16:05
Tu ne sais pas dériver la fonction x-->1/(x+1) ?? Regarde dans ton cours, tu as surement la reponse...
-
Kso
- Membre Naturel
- Messages: 50
- Enregistré le: 02 Nov 2008, 16:54
-
 par Kso » 30 Oct 2009, 16:08
par Kso » 30 Oct 2009, 16:08
Bonjour,
Ben, j'avais déjà essayé en suivant les règles :
f(x) = a -> f'(x) = 0
f(x) = ax+b -> f'(x) = 1
f(x) = 1/x -> f'(x) =1/1²
Et j'ai trouvé 1... J'ai trouvé ça trop stupide pour que ce soit le résultat, mais mais (au vue de vot' réaction...) heu c'est bon ?
-
jameso
- Membre Naturel
- Messages: 62
- Enregistré le: 11 Aoû 2006, 15:12
-
 par jameso » 30 Oct 2009, 16:11
par jameso » 30 Oct 2009, 16:11
Attention la dérivée de f(x)=ax+b est f'(x)=a
la dérivée de g(x)=1/x est g'(x)=-1/x² pour x différent de 0
-
Kso
- Membre Naturel
- Messages: 50
- Enregistré le: 02 Nov 2008, 16:54
-
 par Kso » 30 Oct 2009, 16:29
par Kso » 30 Oct 2009, 16:29
jameso a écrit:Attention la dérivée de f(x)=ax+b est f'(x)=a
la dérivée de g(x)=1/x est g'(x)=-1/x² pour x différent de 0
Attendez, j'ai fait une erreur de signe ??
f(x) = a -> f(x') = 0 donc -
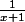
f(x) = ax+b -> f(x') =a donc -
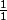
f(x) =

-> f(x') = -
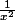
et vu que - et - = +
ça fait 1/1 = 1 ?
-
jameso
- Membre Naturel
- Messages: 62
- Enregistré le: 11 Aoû 2006, 15:12
-
 par jameso » 30 Oct 2009, 16:32
par jameso » 30 Oct 2009, 16:32
Tu dois trouver que la dérivée de f est f'(x)=1/(x+1)² pour x différent de -1
-
Kso
- Membre Naturel
- Messages: 50
- Enregistré le: 02 Nov 2008, 16:54
-
 par Kso » 30 Oct 2009, 16:36
par Kso » 30 Oct 2009, 16:36
Je ne vous suis plus là, pourquoi mon résultat est-il faux ? Et j'ai pas très compris le -1.=/
-
Kso
- Membre Naturel
- Messages: 50
- Enregistré le: 02 Nov 2008, 16:54
-
 par Kso » 30 Oct 2009, 16:36
par Kso » 30 Oct 2009, 16:36
Je ne vous suis plus là, pourquoi mon résultat est-il faux ? Et j'ai pas très compris le -1.=/
-
jameso
- Membre Naturel
- Messages: 62
- Enregistré le: 11 Aoû 2006, 15:12
-
 par jameso » 30 Oct 2009, 16:38
par jameso » 30 Oct 2009, 16:38
Oui ton résultat est faux.. Je te conseille de relire ton cours sur la dérivation car tu ne sembles pas vraiment au point..
-
Kso
- Membre Naturel
- Messages: 50
- Enregistré le: 02 Nov 2008, 16:54
-
 par Kso » 30 Oct 2009, 16:48
par Kso » 30 Oct 2009, 16:48
C'est à dire que je n'ai aucun cours sur les dérivations. Ce DM est intégré aux pôlynomes du second degré mais je n'ai rien sur les dérivés de fonctions (je vous le dis avec le cours entier en main) et j'ai dû chercher les formules sur Internet. Et avant de poster ici, j'ai recherché comment étudier le sens de variation.
-
jameso
- Membre Naturel
- Messages: 62
- Enregistré le: 11 Aoû 2006, 15:12
-
 par jameso » 30 Oct 2009, 17:00
par jameso » 30 Oct 2009, 17:00
On peut s'en sortir autrement: par composition des fonctions de références x--->x+1 et x--->1/x etc.. tu connais surement les variations de ces fonctions de références (cf cours seconde)
-
Kso
- Membre Naturel
- Messages: 50
- Enregistré le: 02 Nov 2008, 16:54
-
 par Kso » 30 Oct 2009, 17:04
par Kso » 30 Oct 2009, 17:04
D'accord, merci :
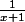
Voilà les fonctions de référence :
x+1 -> fonction affine
1/x -> fonction inverse
Qu'est-ce que vous entendez par composition ?
-
jameso
- Membre Naturel
- Messages: 62
- Enregistré le: 11 Aoû 2006, 15:12
-
 par jameso » 30 Oct 2009, 17:11
par jameso » 30 Oct 2009, 17:11
As-tu déja entendu parler de composition de fonctions :
Soit f la fonction définie par f(x)=x+1 et g définie par g(x)=1/x .Alors pour x différent de -1, g(f(x))=1/(x+1) On a composé les fonctions f et g .Or f est croissante sur R et g décroissante sur R* donc par composition g°f est décroissante sur R privé de -1
Il faut encore travailler un peu pour déduire les variations de f...
Si ça ne te parle pas ça et que la dérivation n'a pas encore été vue je ne peux plus t'aider..
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 30 Oct 2009, 17:20
par benekire2 » 30 Oct 2009, 17:20
Si tu n'as pas vu la dériv, n'utilise pas cette notion!!
regarde bien comment on en a pas besions:
soit a et b deux nombre de
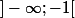
tels que

On a:

or la fonction inverse est décroissante sur
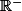
donc:

et donc :

Donc f est Décroissante sur cet intervalle, tu fais pareil pour l'autre et tu trouvera décroissant aussi.
-
jameso
- Membre Naturel
- Messages: 62
- Enregistré le: 11 Aoû 2006, 15:12
-
 par jameso » 30 Oct 2009, 17:22
par jameso » 30 Oct 2009, 17:22
Exact, en revenant à la définition d'une fonction croissante/décroissante on peut s'en sortit facilement. Autant pour moi..
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 30 Oct 2009, 17:22
par benekire2 » 30 Oct 2009, 17:22
Cette méthode ne marchera pas pour les choses plus dure, mais là ca fonctionne parfaitement.
Après, il faut savoir aussi, que tu as dû voir une méthode avec les composées que l'on aurait pu appliqué ici, mais qui est trop longue et généralement inutile, car si c'est faisable avec les variations de composé, c'est toujours faisable par cette méthode.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 30 Oct 2009, 17:25
par benekire2 » 30 Oct 2009, 17:25
Je suppose donc que ta question suivante sera d'étudier la position d'une droite par rapport à ton hyperbole...
Alors point méthode qui marche tout le temps:
Pour étudier la position de y par rapport a Cf on étudie le signe de f(x)-y et là trois cas:
f(x)-y >0 f au dessus de y
f(x)-y =0 points d'intersection
f(x)-y <0 f au dessous de y
Et voilà !
-
Kso
- Membre Naturel
- Messages: 50
- Enregistré le: 02 Nov 2008, 16:54
-
 par Kso » 30 Oct 2009, 17:26
par Kso » 30 Oct 2009, 17:26
Oui, ça me parle. On a fait ça au 1er chapitre. Avec les vou et uov et tout ça ? Oui, seulement ça m'étais sorti de la tête. Mais j'avoue ne pas être très à l'aise avec. Mais je pense, tout de même, avoir compris ce que vous voulez dire.
F(x)est croissante en R puisqu'elle conserve l'ordre.
G(x) est décroissante en R*( -1 est exclu) puisqu'elle ne conserve pas l'ordre.
L'ordre n'est pas conservé donc la fonction g(f(x)) est décroissante sur R.
Attendez, pour le reste je vais reprendre mon cours, afin d'éviter toutes erreurs possibles.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités
