Halloween sous le signe des maths

[dogblue]

Bonsoir à tous
J'ai un exercice de maths à faire en DM, et pour l'instant je bloque un peu. L'exercice est un "problème ouvert". Voilà l'énoncé :

Pour Halloween, Amélie prépare un sac de friandises qui contient 10 réglisses, et 30 bonbons aux fruits. Chaque fois qu'un enfant prend un bonbon dans son sac, Amélie ajoute un réglisse dans le sac.
A partir de combien de prélèvements,la probabilité de tomber sur un réglisse devient-elle supérieure à 0.32 ?

J'ai commencer par faire un arbre, et j'en ai déduit que cela se passait à partir de 5 bonbons tirés. Or je dois justifier ce résultat par calcul, et c'est la que j'ai du mal.

Voila, j'espère que vous m'aiderez avec quelques pistes !
Merci d'avance. Bonne soirée =)

[nodjim]

La proba de tomber sur un réglisse sera de 0.32 quand dans le sac il y aura

[nodjim]

La proba de tomber sur un réglisse sera de 0.32 quand dans le sac il y aura 32% de réglisses.

[dogblue]

La proba de tomber sur un réglisse sera de 0.32 quand dans le sac il y aura 32% de réglisses.

Oui je l'ai bien compris, mais je n'arrive pas à le traduire en calcul.
Je pense qu'il faut d'abord définir une suite, et utiliser la fonction pour résoudre l'inégalité.

[Waax22951]

Ah, on a le même livre d'exercices..! :lol3:
On considère, pour tout entier n supérieur ou égal à 1, la suite d’événements suivant:
: "Le bonbon prélevé au n-ième prélèvement est un bonbon à la réglisse"
On considère aussi la suite définie par .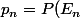
Avec un arbre tu peux trouver une valeur de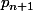 en fonction de . Après tu peux résoudre le problème avec un algorithme et en montrant que la suite est croissante.

Bonne soirée :we:

[dogblue]

Ah, on a le même livre d'exercices..! :lol3:
On considère, pour tout entier n supérieur ou égal à 1, la suite d’événements suivant:
: "Le bonbon prélevé au n-ième prélèvement est un bonbon aux fruits"
On considère aussi la suite définie par .
Avec un arbre tu peux trouver une valeur de en fonction de . Après tu peux résoudre le problème avec un algorithme et en montrant que la suite est croissante.

Bonne soirée :we:

pour calculer n+1, il faut distinguer 2cas non ?!

[dogblue]

E_n: "Le bonbon prélevé au n-ième prélèvement est un bonbon aux fruits"
n'est il pas mieux de prendre pour un réglisse ?

[dogblue]

et pour l'algorythme j'ai du mal a comprendre le apport entre les différents tirages

[Waax22951]

E_n: "Le bonbon prélevé au n-ième prélèvement est un bonbon aux fruits"
n'est il pas mieux de prendre pour un réglisse ?

Oui en effet, j'ai fait une faute dans ma réponse, j'ai confondu les deux bonbons..!
Du coup je vais corriger mon post.

On remarque qu'on a:

Après tu peux obtenir chaque probabilité à l'aide d'un arbre :lol3:
Tu fais un algorithme pour résoudre l'inéquation , ou alors tu peux aussi juste remarquer que cela se produit lorsque

Bonne soirée :lol3:

[dogblue]

Oui en effet, j'ai fait une faute dans ma réponse, j'ai confondu les deux bonbons..!
Du coup je vais corriger mon post.

On remarque qu'on a:

Après tu peux obtenir chaque probabilité à l'aide d'un arbre :lol3:
Tu fais un algorithme pour résoudre l'inéquation , ou alors tu peux aussi juste remarquer que cela se produit lorsque

Bonne soirée :lol3:

Je comprend mieux tout ca, par contre au lieu de définir En,En+1 , est ce qu'on peut juste dire que Pn est la proba de tirer un réglisse ? ainsi ca simplifierai les calculs non ?

[dogblue]

Je comprend mieux tout ca, par contre au lieu de définir En,En+1 , est ce qu'on peut juste dire que Pn est la proba de tirer un réglisse ? ainsi ca simplifierai les calculs non ?

Serait ce possible aussi, d'utiliser cette suite en la transformant en fonction, pour résoudre l'inégalité ?

[Waax22951]

Serait ce possible aussi, d'utiliser cette suite en la transformant en fonction, pour résoudre l'inégalité ?

Non car il s'agit d'une suite qui est de la forme où f est une fonction définie (ici c'est une fonction affine par exemple). Du coup tu ne connais pas l'expression de en fonction de n pour savoir à partir quel rang n on a :lol3:

[Ben314]

Salut,
Juste une question : l'énoncé c'est bien ça

Chaque fois qu'un enfant prend un bonbon dans son sac, Amélie ajoute un réglisse dans le sac.

et pas ça

Chaque fois qu'un enfant prend une friandise dans son sac, Amélie ajoute un réglisse dans le sac.

?

(avec la version 1, c'est quand même pas mal compliqué...)

[dogblue]

Salut,
Juste une question : l'énoncé c'est bien ça et pas ça ?

(avec la version 1, c'est quand même pas mal compliqué...)

Voila la bonne version "Chaque fois qu'un enfant prend une friandise dans son sac, Amélie ajoute un réglisse dans le sac."

[Ben314]

Merci.
C'est effectivement infiniment plus simple avec cet énoncé là...

[dogblue]

Merci.
C'est effectivement infiniment plus simple avec cet énoncé là...

Infiniement plus simple, mais j'ai tout de même à établir les calculs..

[Waax22951]

Merci.
C'est effectivement infiniment plus simple avec cet énoncé là...

En effet, je n'avais pas vu l'énoncé puisque je l'avais déjà fait donc je l'ai juste survolé, mais le problème est beaucoup plus compliqué si on considère l'autre énoncé..!
Qu'as-tu fait exactement ? :lol3:

[Ben314]

Merci.
C'est effectivement infiniment plus simple avec cet énoncé là...

Ne te méprend pas sur ce que j'ai voulu dire : tel quel ça me semble un problème franchement ardu pour des Lycéens.

Mais avec l'autre énoncé ou on ne remettait pas systématiquement des réglisses dans le sac, là, c'était vraiment pas raisonnable...

Sinon, concernant la façon de mener les calculs, je pense que Waax22951 t'a donné déjà pas mal d'informations (pas complètement toute, mais presque...)