Guide Equation - Inéquations - Systèmes [Inachevé]
72 messages
- Page 1 sur 4 - 1, 2, 3, 4
Guide Equation - Inéquations - Systèmes [Inachevé]
Bonjour à vous !
Sujet récurrent sur le forum, les équations posent encore beaucoup de problème là où il ne devrait pas y en avoir.
Pour remédier à cela, je vous propose donc un guide (incomplet pour linstant mais que je complèterai le plus vite possible) qui traite de la résolution déquation, dinéquations et des systèmes linéaires.
Je me suis efforcé de détailler au mieux les raisonnement à adopter afin de résoudre ces différentes équations inéquations et/ou systèmes rencontrés de la 2nde jusquà la Tle S.
Bien évidemment, je suis tout à fait conscient que tout le monde nest pas aussi à laise avec la théorie que dautres, cest pourquoi je mappuierai en particulier sur des exemples concrets.
De même, pour une compréhension universelle, je privilégierai lemploi du français à certains symboles mathématiques pour plus de clarté.
Il est bien entendu que ce guide a pour but dapporter une aide et non pas de faire votre travail à votre place.
Jespère que ce guide vous sera fort utile et que vous serez pleinement satisfait.
Nhésitez pas à me contacter en cas dincompréhension ou derreur(s) éventuelle(s) de ma part.
(Je remercie Lostounet pour la précieuse aide qu'il m'a apportée sur ce projet)
Pour commencer, veuiller choisir votre rubrique de résolution :
[CENTER] [/CENTER]
Sujet récurrent sur le forum, les équations posent encore beaucoup de problème là où il ne devrait pas y en avoir.
Pour remédier à cela, je vous propose donc un guide (incomplet pour linstant mais que je complèterai le plus vite possible) qui traite de la résolution déquation, dinéquations et des systèmes linéaires.
Je me suis efforcé de détailler au mieux les raisonnement à adopter afin de résoudre ces différentes équations inéquations et/ou systèmes rencontrés de la 2nde jusquà la Tle S.
Bien évidemment, je suis tout à fait conscient que tout le monde nest pas aussi à laise avec la théorie que dautres, cest pourquoi je mappuierai en particulier sur des exemples concrets.
De même, pour une compréhension universelle, je privilégierai lemploi du français à certains symboles mathématiques pour plus de clarté.
Il est bien entendu que ce guide a pour but dapporter une aide et non pas de faire votre travail à votre place.
Jespère que ce guide vous sera fort utile et que vous serez pleinement satisfait.
Nhésitez pas à me contacter en cas dincompréhension ou derreur(s) éventuelle(s) de ma part.
(Je remercie Lostounet pour la précieuse aide qu'il m'a apportée sur ce projet)
Pour commencer, veuiller choisir votre rubrique de résolution :
[CENTER] [/CENTER]
Veuillez choisir le type d'équation auquel vous êtes confronté :
1°) Equation polynômiale
2°) Equation rationnelle
3°) Equation irrationnelle
4°) Equation trigonométrique
5°) Equation valeur absolue
6°) Equation se ramenant à un changement de variable
7°) Equation Puissance
8°) Equation où figure des logarithmes népériens (ou naturels)
9°) Equation où figure des exponentielles
10°) Equation dans l'ensemble des complexes
11°) Equation diophantienne
12°) Equation où figure des PGCD et/ou des PPCM
13°) Equation différentielle
14°) Equation fonctionnelle
15°) Equation bizarre
Veuillez choisir le type d'inéquation auquel vous êtes confronté :
1°) Inequation polynômiale
2°) Inéquation rationnelle
3°) Inéquation irrationnelle
4°) Inéquation trigonométrique
5°) Inéquation valeur absolue
6°) Inéquation se ramenant à un changement de variable
7°) Inéquation Puissance
8°) Inéquation où figure des logarithmes népériens (ou naturels)
9°) Inéquation où figure des exponentielles
10°) Inéquation bizarre
Veuillez choisir le type de système auquel vous êtes confronté :
1°) 2 équations à 2 inconnues
2°) 3 équations à 3 inconnues
3°) 4 équations à 4 inconnues
4°) Système plus complexes
1°) Equation polynômiale
Parmi les équations polynomiales, choisissez celle qui vous convient :
a) Trinome du second degré
b) Polynôme de degré 3 ou 4
c) Equation Bicarrée
Parmi les équations polynomiales, choisissez celle qui vous convient :
a) Trinome du second degré
b) Polynôme de degré 3 ou 4
c) Equation Bicarrée
a) Trinôme du second degré
On appelle équation trinôme du second degré toute équation de la forme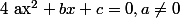 sinon ce n'est pas le cas. Soit
sinon ce n'est pas le cas. Soit ) une telle équation.
une telle équation.
Au trinôme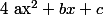 on associe un réel
on associe un réel 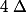 appelé discriminant défini par
appelé discriminant défini par 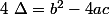 .
.
Par suite, suivant les valeurs des coefficients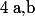 et
et 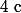 , on distingue trois cas :
, on distingue trois cas :
- Si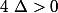 alors l'équation
alors l'équation ) admet deux solutions distinctes définies par :
admet deux solutions distinctes définies par :
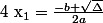 et
et 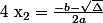
- Si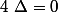 alors l'équation
alors l'équation ) admet une solution :
admet une solution :
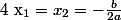
- Si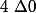 par conséquent :
par conséquent :
+\sqrt{9}}{2\times 2}=\frac{5}{2}) et
et -\sqrt{9}}{2\times 2}=1)
Donc
2°) (
( ,
, 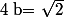 ,
, 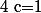 )
)
^2-4\times \frac{1}{2}\times 1=2-2=0)
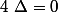 par conséquent :
par conséquent :
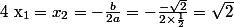
Donc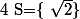
3°)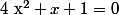 (
(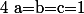 )
)
^2-4\times 1\times 1=1-4=-3)
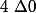 .
.
Or quel que soit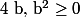 par cosnéquent
par cosnéquent 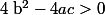 d'où
d'où 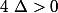 donc
donc ) admet nécessairement deux solutions distinctes.
admet nécessairement deux solutions distinctes.
De même, si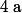 et
et 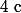 sont de signe différent alors
sont de signe différent alors  , par conséquent, on a d'après la formule sur le produit des racines
, par conséquent, on a d'après la formule sur le produit des racines 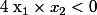 donc on peut affirmer que
donc on peut affirmer que 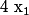 et
et 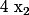 sont de signe différent.
sont de signe différent.
On retiendra donc que si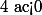 alors
alors ) admet deux solutions distinctes de signe différent.
admet deux solutions distinctes de signe différent.
On appelle équation trinôme du second degré toute équation de la forme
Au trinôme
Par suite, suivant les valeurs des coefficients
- Si
- Si
- Si
Donc
2°)
Donc
3°)
Or quel que soit
De même, si
On retiendra donc que si
a) Polynôme de degré 3 ou 4
On appelle équation polynomiale de degré toute équation de la forme :
toute équation de la forme :
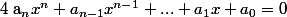 , avec
, avec 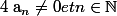
La famille de réels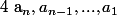 et
et 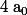 sont appelés coefficients du polynôme
sont appelés coefficients du polynôme 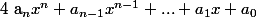 .
.
Le degré d'un polynôme est égal au degré de son monôme de plus haut degré.
est égal au degré de son monôme de plus haut degré.
Exemples :
-=x^5+2x+1) ,
,  a le même degré que le monôme
a le même degré que le monôme 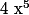 donc
donc  est de degré 5.
est de degré 5.
-=4) ,
,  est de degré 0 car
est de degré 0 car 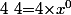
-=0) , c'est le polynôme nul, il n'a pas de degré.
, c'est le polynôme nul, il n'a pas de degré.
Si et
et 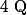 sont deux polynôme de degré respectifs
sont deux polynôme de degré respectifs 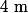 et
et  alors le polynôme
alors le polynôme 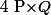 est de degré
est de degré 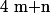
Exemple :(x^3-1))
Si=x^7+x^2-1) et
et =x^3-1) alors
alors 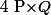 est de degré 7+3=10
est de degré 7+3=10
Deux polynômes sont égaux si et seulement si ils ont le même degré et les mêmes coefficients :
Si et
et 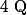 sont deux polynôme de même degré
sont deux polynôme de même degré  tels que :
tels que :
=a_n x^n + a_{n-1} x^{n-1}+...+a_1 x+a_0)
et
=b_n x^n + b_{n-1} x^{n-1}+...+b_1 x+b_0)
alors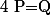 équivaut à
équivaut à 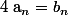 ;
; 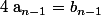 ; ... ;
; ... ; 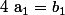 et
et 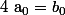 .
.
Soit un polynôme de degré
un polynôme de degré  et
et 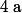 un réel.
un réel.
Si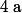 est une racine (ou un "zéro") d'un polynôme
est une racine (ou un "zéro") d'un polynôme  alors
alors =0)
Si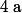 est une racine (ou un "zéro") du polynôme
est une racine (ou un "zéro") du polynôme  alors il existe un Polynôme
alors il existe un Polynôme 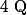 de degré
de degré 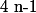 tel que, pour tout
tel que, pour tout  réel :
réel : =(x-a)Q(x))
Déterminer les racines d'un polynôme équivaut à résoudre
équivaut à résoudre =0)
Pour trouver toutes les racines d'un polynôme, il faut d'abord commencer par trouver des racines dites évidentes, c'est-à-dire, qu'on calcule 4$ P(x) pour toutes les valeurs entières de comprises entre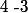 et
et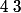 , ensuite on se servira du trinôme du second degré.
, ensuite on se servira du trinôme du second degré.
Pour un polynôme de degré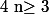 , il est nécessaire de trouver
, il est nécessaire de trouver 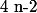 racines évidentes.
racines évidentes.
Enfin, un polynôme de degré admet dans
admet dans 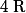 au plus
au plus  racines disitnctes.
racines disitnctes.
Exemple :
Déterminer les racines du polynôme=2x^4-5x^3-15x^2+10x+8)
 est de degré 4 par conséquent, il faut trouver 4-2=2 racines évidentes.
est de degré 4 par conséquent, il faut trouver 4-2=2 racines évidentes.
si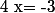 alors
alors \neq 0) , donc
, donc 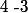 n'est pas une racine de
n'est pas une racine de  .
.
si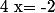 alors
alors = 0) , donc
, donc 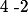 est une pas racine de
est une pas racine de  .
.
si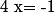 alors
alors \neq 0) , donc
, donc 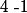 n'est pas une racine de
n'est pas une racine de  .
.
si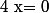 alors
alors \neq 0) , donc
, donc 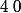 n'est pas une racine de
n'est pas une racine de  .
.
si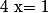 alors
alors =1) , donc
, donc 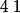 est une racine de
est une racine de  .
.
=P(1)=0) donc il existe un polynôme
donc il existe un polynôme 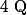 . de degré 4-2=2 tel que que pour tout réel
. de degré 4-2=2 tel que que pour tout réel  :
:
=(x-1)(x+2)Q(x))
avec=ax^2+bx+c)
Déterminons alors les coefficients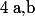 et
et 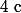 :
:
Pour tout x réel :
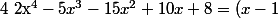(x+2)(ax^2+bx+c))
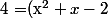(ax^2+bx+c))
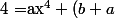x^3+(c+b-2a)x^2+(c-2b)x-2c)
Par identification, cela équivaut à :
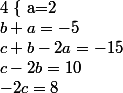
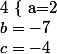
Donc pour tout=2x^2-7x-4)
On résous=0) grâce au trinôme du second degré :
grâce au trinôme du second degré :
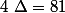 donc
donc 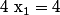 et
et 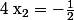
Donc
On appelle équation polynomiale de degré
La famille de réels
Le degré d'un polynôme
Exemples :
-
-
-
Si
Exemple :
Si
Deux polynômes sont égaux si et seulement si ils ont le même degré et les mêmes coefficients :
Si
et
alors
Soit
Si
Si
Déterminer les racines d'un polynôme
Pour trouver toutes les racines d'un polynôme, il faut d'abord commencer par trouver des racines dites évidentes, c'est-à-dire, qu'on calcule 4$ P(x) pour toutes les valeurs entières de comprises entre
Pour un polynôme de degré
Enfin, un polynôme de degré
Exemple :
Déterminer les racines du polynôme
si
si
si
si
si
avec
Déterminons alors les coefficients
Pour tout x réel :
Par identification, cela équivaut à :
Donc pour tout
On résous
Donc
c) Equation bicarrées
On appelle équation bicarrée, toute équation de la forme :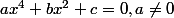 .
.
Les équations bicarrées sont un cas particulier d'équations se ramenant à un changement de variable en posant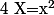 .
.
Une fois ce changement de variable effectué, il n'y a plus qu'à résoudre une équation trinôme.
Exemple :
1°) Résoudre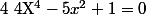
On pose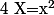 et on résous
et on résous 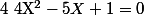
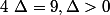 donc
donc 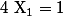 et
et 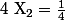
Or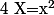 donc on résous
donc on résous 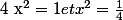
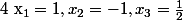 et
et 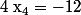
Donc
2°) Résoudre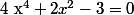
On pose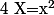 et on résous
et on résous 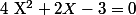
On peut voir une racine évidente :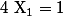
Or d'après la formule sur le produit des racines :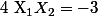 , donc
, donc 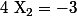
Ensuite, sachant que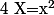 on résous
on résous 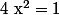 et
et 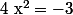
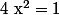 donc
donc 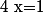 ou
ou 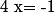
Or pour tout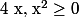 , l'équation
, l'équation 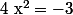 n'admet donc aucune solution.
n'admet donc aucune solution.
Donc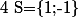
Remarques :
1°) Si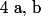 et
et 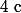 sont strictement positifs alors il n'y a pas de solutions.
sont strictement positifs alors il n'y a pas de solutions.
2°) Si l'équation est "incomplète" on n'effectuera pas de changement de variable et on n'utilisera pas le discriminant.
Exemple :
-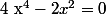
=0)
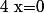 ou
ou 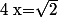 ou
ou 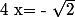
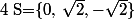
-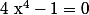
(x^2+1)=0)
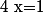 ou
ou 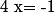
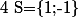
On appelle équation bicarrée, toute équation de la forme :
Les équations bicarrées sont un cas particulier d'équations se ramenant à un changement de variable en posant
Une fois ce changement de variable effectué, il n'y a plus qu'à résoudre une équation trinôme.
Exemple :
1°) Résoudre
On pose
Or
Donc
2°) Résoudre
On pose
On peut voir une racine évidente :
Or d'après la formule sur le produit des racines :
Ensuite, sachant que
Or pour tout
Donc
Remarques :
1°) Si
2°) Si l'équation est "incomplète" on n'effectuera pas de changement de variable et on n'utilisera pas le discriminant.
Exemple :
-
-
2°) Equation rationnelle
On appelle équation rationnelle toute équation de la forme :
}{Q(x)}=0) où
où  et
et 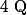 désigne des polynômes et
désigne des polynômes et \neq 0) .
.
Attention : Ce genre d'équation peut-être écrite sous différente forme qu'il faut exprimer sous un dénominateur commun.
Exemple : (On suppose pour chaque équation le domaine établit)
- l'équation devient
devient  qui est bien une équation rationnelle
qui est bien une équation rationnelle
- l'équation a beau devenir
a beau devenir 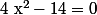 elle est rationnelle.
elle est rationnelle.
- l'équation devient
devient  et est donc bien rationnelle.
et est donc bien rationnelle.
- devient
devient  qui est bien rationnelle.
qui est bien rationnelle.
L'équation est dite rationnelle si et seulement si l'inconnue se trouve au dénominateur.
Ainsi, bien que l'équation n'admette aucune solution, elle est bien rationnelle.
n'admette aucune solution, elle est bien rationnelle.
Pour résoudre ce genre d'équation, on établit avant toute chose le domaine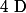 de définition de l'équation qui défini pour quelle(s) valeur(s) de l'inconnue, l'équation n'a pas de sens.
de définition de l'équation qui défini pour quelle(s) valeur(s) de l'inconnue, l'équation n'a pas de sens.
Rappel : Un dénominateur n'est jamais nul.
Ensuite, si l'équation ne se présente pas sous la forme}{Q(x)}=0) alors il faut ordonner et réduire tout d'un même côté pour obtenir cette forme.
alors il faut ordonner et réduire tout d'un même côté pour obtenir cette forme.
Enfin, quel que soit de l'ensemble
de l'ensemble 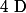 , résoudre
, résoudre }{Q(x)}=0) équivaut à résoudre
équivaut à résoudre =0) .
.
Une fois les solutions trouvées, on vérifie bien qu'elles appartiennent à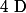 .
.
Exemple : Résoudre
1°)
Cette équation est définie si et seulement si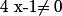
On résous donc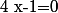 et on trouve
et on trouve 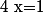 .
.
PAr conséquent, le domaine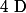 de cette équation est
de cette équation est 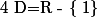 .
.
Pour tout de
de 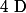 :
:  équivaut à
équivaut à 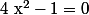 et on trouve donc
et on trouve donc 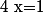 ou
ou 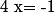 .
.
Or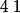 n'appartient pas à
n'appartient pas à 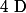 donc
donc 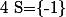
2°)
Cette équation est définie si et seulement si :
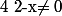 et
et 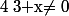
Par conséquent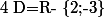
Pour tout de
de 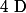 :
:  équivaut à
équivaut à
(3+x)=(3+2x)(2-x)) grâce au produit en croix
grâce au produit en croix
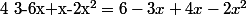
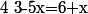
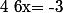

 appartient bien à
appartient bien à 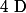 donc
donc 
3°)
Cette équation est définie si et seulement si n'est pas nul donc
n'est pas nul donc 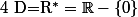
Pour tout de
de 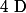 :
:  équivaut à
équivaut à
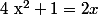
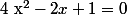
^2=0)
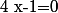
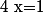
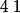 appartient bien à
appartient bien à 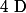 donc
donc 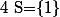
4°)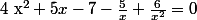
Cette équation est définie si et seulement si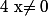 et
et 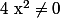 .
.
Par conséquent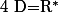
Pour tout de
de 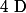 :
: 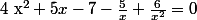 équivaut à
équivaut à
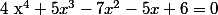
Il y a deux racines évidentes :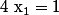 et
et 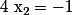 .
.
Par conséquent il existe un trinôme du second degré tel que, pour tout
du second degré tel que, pour tout  de
de 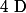 :
:
(x+1)P(x))
avec=ax^2+bx+c)
Pour tout de
de 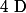 :
:
(x+1)P(x))
(ax^2+bx+c))
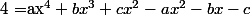
x^2-bx-c)
Par identification :
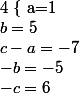
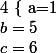
Donc=x^2+5x-6)
On résous=0)
Il y a une racine évidente :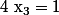 or d'après la formule sur le produit des racines :
or d'après la formule sur le produit des racines : 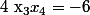 , donc
, donc 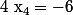 .
.
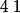 ,
, 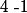 et
et 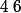 appartiennent bien à
appartiennent bien à 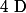 donc
donc 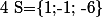
On appelle équation rationnelle toute équation de la forme :
Attention : Ce genre d'équation peut-être écrite sous différente forme qu'il faut exprimer sous un dénominateur commun.
Exemple : (On suppose pour chaque équation le domaine établit)
- l'équation
- l'équation
- l'équation
-
L'équation est dite rationnelle si et seulement si l'inconnue se trouve au dénominateur.
Ainsi, bien que l'équation
Pour résoudre ce genre d'équation, on établit avant toute chose le domaine
Rappel : Un dénominateur n'est jamais nul.
Ensuite, si l'équation ne se présente pas sous la forme
Enfin, quel que soit
Une fois les solutions trouvées, on vérifie bien qu'elles appartiennent à
Exemple : Résoudre
1°)
Cette équation est définie si et seulement si
On résous donc
PAr conséquent, le domaine
Pour tout
Or
2°)
Cette équation est définie si et seulement si :
Par conséquent
Pour tout
3°)
Cette équation est définie si et seulement si
Pour tout
4°)
Cette équation est définie si et seulement si
Par conséquent
Pour tout
Il y a deux racines évidentes :
Par conséquent il existe un trinôme
avec
Pour tout
Par identification :
Donc
On résous
Il y a une racine évidente :
3°) Equation irrationnelle
On appelle équation irrationnelle, toute équation de la forme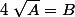 , avec
, avec 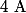 et
et 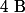 deux expressions en fonction de
deux expressions en fonction de  , qui peut se ramener sous la forme d'une équation polynômiale de la forme
, qui peut se ramener sous la forme d'une équation polynômiale de la forme =0) .
.
Pour résoudre une équation de la forme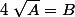 équivaut à résoudre le système
équivaut à résoudre le système 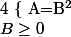
Exemples : Résoudre :
1°)
Cela équivaut à résoudre\\ 2\ge 0)
On résous) :
:
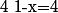
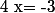
Or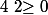 est toujours vérifiée donc
est toujours vérifiée donc 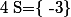
2°)
Cela équivaut à résoudre\\ x\ge 0)
On résous) :
:
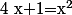
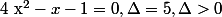 donc :
donc :
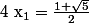 ou
ou 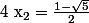
Or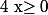 et
et 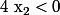 donc
donc 
3°)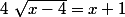
Cela équivaut à résoudre^2 \quad (1)\\ x+1\ge 0)
On résous) :
:
^2)
^2-x+4=0)
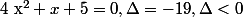 donc l'équation n'a pas de solution et donc le système non plus :
donc l'équation n'a pas de solution et donc le système non plus : 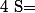
Remarque :
a) Il est inutile d'établir le domaine de A sous la racine.
b) Si l'équation n'admet aucune solution ou si l'inéquation n'est jamais vérifiée alors le système n'admet pas de solution
On appelle équation irrationnelle, toute équation de la forme
Pour résoudre une équation de la forme
Exemples : Résoudre :
1°)
Cela équivaut à résoudre
On résous
Or
2°)
Cela équivaut à résoudre
On résous
Or
3°)
Cela équivaut à résoudre
On résous
Remarque :
a) Il est inutile d'établir le domaine de A sous la racine.
b) Si l'équation n'admet aucune solution ou si l'inéquation n'est jamais vérifiée alors le système n'admet pas de solution
4°) Equation trigonométrique
On rappelle que quels que soient les réels x, a et b :
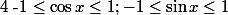
=\cos x ; \sin(-x)= - \sin x)
= - \cos x ; \sin(\pi - x)= \sin x)
= - \cos x ; \sin(\pi + x)= \sin x)
= \sin x ; \sin\( \frac{\pi}{2} - x\)= \cos x)
= - \sin x ; \sin\( \frac{\pi}{2}+ x\)= \cos x)
=\cos a \cos b + \sin a \sin b)
=\cos a \cos b - \sin a \sin b)
=\sin a \cos b - \sin b \cos a)
=\sin a \cos b + \sin b \cos a)
On rappelle également les valeurs reamrquables :

I : Equation de la forme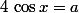
Si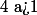 ou
ou 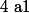 ou
ou 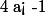 alors l'équation n'admet aucune solution.
alors l'équation n'admet aucune solution.
Si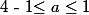 alors il existe un unique réel
alors il existe un unique réel 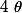 de
de  tel que :
tel que : 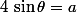 .
.
On résous ainsi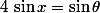
Cette équation équivaut à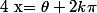 ou
ou 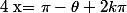 avec
avec 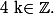
III : Equation de la forme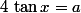
(à venir)
Exemple : Résoudre dans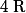
1°)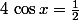
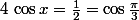 équivaut à
équivaut à
 ou
ou 
Donc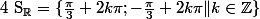
2°)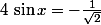
) équivaut à
équivaut à
 ou
ou 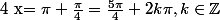
Donc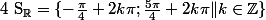
Remarque :
a) Pour résoudre des équations trigonométrique (tout comme les logarithmes) il faut impérativement arrivé à \cos ... = \cos ... ou \sin ...=\sin ...
b) Quel que fois, on demandera de résoudre dans un intervalle donné ce genre d'équation. On la résolvera d'abord dans R puis, suivant l'intervalle, on devra choisir une ou des valeurs de k pour lesquelles les solutions appartiennent à cet intervalle.
Exemple : Si on veut résoudre l'équation du 1°) dans alors on cherche les valeurs de l'entier k pour lesquelles
alors on cherche les valeurs de l'entier k pour lesquelles  .
.
Or on a établit que ou
ou 
Donc équivaut à
équivaut à
 ou
ou 
On divise tout par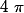 :
:
 ou
ou 
 ou
ou 
 ou
ou 
Or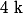 est un entier (appartient à
est un entier (appartient à  )
)
Donc il n'y a qu'une valeur de k (k=0) pour laquelle l'éqation admet une solution dans qui est donc :
qui est donc :
) ou
ou )
Donc
On rappelle que quels que soient les réels x, a et b :
On rappelle également les valeurs reamrquables :
I : Equation de la forme
Si
Si
On résous ainsi
Cette équation équivaut à
III : Equation de la forme
(à venir)
Exemple : Résoudre dans
1°)
Donc
2°)
Donc
Remarque :
a) Pour résoudre des équations trigonométrique (tout comme les logarithmes) il faut impérativement arrivé à \cos ... = \cos ... ou \sin ...=\sin ...
b) Quel que fois, on demandera de résoudre dans un intervalle donné ce genre d'équation. On la résolvera d'abord dans R puis, suivant l'intervalle, on devra choisir une ou des valeurs de k pour lesquelles les solutions appartiennent à cet intervalle.
Exemple : Si on veut résoudre l'équation du 1°) dans
Or on a établit que
Donc
On divise tout par
Or
Donc il n'y a qu'une valeur de k (k=0) pour laquelle l'éqation admet une solution dans
Donc
6°) Equation se ramenant à un changement de variable
On utilise parfois un procédé appelé changement de variable qui permet de résoudre plus facilement voire plus rapidement une équation en évitant des calculs fastidieux.
On peut noter que ce changement de variable concerne souvent le trinôme du second degré.
Voir également les équations Bicarrées
Exemples :
a) Pour résoudre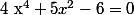 , on peut effectuer le changement de variable
, on peut effectuer le changement de variable 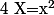 puis résoudre
puis résoudre 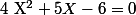
b) Pour résoudre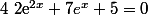 , on peut effectuer le changement de variable
, on peut effectuer le changement de variable 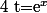 puis résoudre
puis résoudre 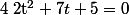
c) Pour résoudre^4-3\( \frac{1}{\sqrt x} \)^2+2=0) , on peut effectuer le changement de variable
, on peut effectuer le changement de variable ^2=\frac{1}{x}) puis résoudre
puis résoudre 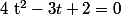
d) Pour résoudre^2-8\(\int_0^{t} e^{\frac{x^2}{2}} \quad dx\)-1=0) , on peut effectuer le changement de variable
, on peut effectuer le changement de variable 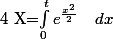 puis résoudre
puis résoudre 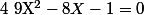
e) Pour résoudre^3+\(\frac{4x-4}{2x+1}\)^2+\frac{1-x}{8x-4}+7=0) , on peut effectuer le changement de variable
, on peut effectuer le changement de variable  puis résoudre
puis résoudre 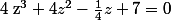
f) Pour résoudre^2=x^2+x+2) , on peut effectuer le changement de variable
, on peut effectuer le changement de variable 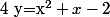 puis résoudre
puis résoudre 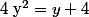 car
car +4) .
.
g) Pour résoudre\cos x -\sqrt 2=0) , on peut effectuer le changement de variable
, on peut effectuer le changement de variable 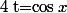 puis résoudre
puis résoudre t - \sqrt 2=0)
Remarque :
a) parfois dans certains exercices, le changement de variable à effectuer sera précisé.
b) avant d'établir le changement de variable, ne pas oublié d'établir le domaine s'il est nécessaire
On utilise parfois un procédé appelé changement de variable qui permet de résoudre plus facilement voire plus rapidement une équation en évitant des calculs fastidieux.
On peut noter que ce changement de variable concerne souvent le trinôme du second degré.
Voir également les équations Bicarrées
Exemples :
a) Pour résoudre
b) Pour résoudre
c) Pour résoudre
d) Pour résoudre
e) Pour résoudre
f) Pour résoudre
g) Pour résoudre
Remarque :
a) parfois dans certains exercices, le changement de variable à effectuer sera précisé.
b) avant d'établir le changement de variable, ne pas oublié d'établir le domaine s'il est nécessaire
8°) Equation où figure des logarithmes népériens (ou naturels)
Il s'agit des équation où l'inconnue figure dans des "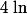 ".
".
On rappelle que cette fonction est définie sur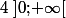 .
.
Quel que soit les réels strictements posititifs a et b,c,d,...,n :
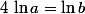 équivaut à
équivaut à 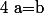
=\ln a +\ln b)
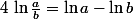
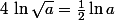
=\ln a +\ln b+\ln c+...\ln n)
Si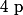 désigne un entier relatif alors
désigne un entier relatif alors 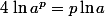
Exemples : Résoudre :
1°)=\ln(x^2+1))
Cette équation est définie si et seulement si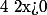 et
et 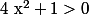 , donc
, donc 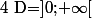 .
.
Pour tout x de D :
=\ln(x^2+1)) équivaut à
équivaut à 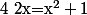
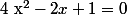
^2=0)
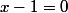

Or 1 appartient bien à D donc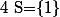
2°)- \frac{1}{2}\ln x)
Cette équation est définie si et seulement si :
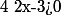 et
et 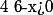 et
et 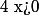
donc et
et 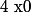 par conséquent
par conséquent  .
.
Pour tout x de D :- \frac{1}{2}\ln x)
équivaut à
=\ln(6-x)- \frac{1}{2}\ln x)
=2\ln(6-x)- \ln x)
=\ln{\((6-x)^2\)}-\ln x)
+\ln x=\ln{\((6-x)^2\)})
)=\ln{\((6-x)^2\)})
=\ln(x^2-12x+36))
équivaut à
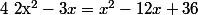
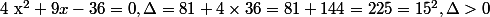
par conséquent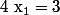 ou
ou 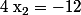 or
or 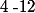 n'appartient pas à D donc
n'appartient pas à D donc 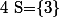
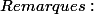
a) Ne pas croire que les deux membres de l'inégalité=\ln a +\ln b) ont le même domaine,
ont le même domaine, ) est défini si et seulement si ab>0 alors que
est défini si et seulement si ab>0 alors que 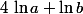 n'est défini que si et seulement si a>0 et b>0.
n'est défini que si et seulement si a>0 et b>0.
b) Ne prendre le logarithme d'un nombre qu'après s'être assuré au préalable qu'il est positif !
Il s'agit des équation où l'inconnue figure dans des "
On rappelle que cette fonction est définie sur
Quel que soit les réels strictements posititifs a et b,c,d,...,n :
Si
Exemples : Résoudre :
1°)
Cette équation est définie si et seulement si
Pour tout x de D :
Or 1 appartient bien à D donc
2°)
Cette équation est définie si et seulement si :
donc
Pour tout x de D :
équivaut à
équivaut à
par conséquent
a) Ne pas croire que les deux membres de l'inégalité
b) Ne prendre le logarithme d'un nombre qu'après s'être assuré au préalable qu'il est positif !
72 messages
- Page 1 sur 4 - 1, 2, 3, 4
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
