Gros Dm sur les suites ( Fibonacci)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
rudy196
- Membre Naturel
- Messages: 14
- Enregistré le: 28 Sep 2015, 21:10
-
 par rudy196 » 30 Sep 2015, 17:29
par rudy196 » 30 Sep 2015, 17:29
Oui merci maintenant e vois pas comment on peut prouver que

p^n+1 +µ(1-p)^n+1+;)p^n +µ(1-p)^n =;)p^n+2 +µ(1-p)^n+2

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 30 Sep 2015, 17:42
par zygomatique » 30 Sep 2015, 17:42
je t'ai dit comment à 20h09 .... par récurrence ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
rudy196
- Membre Naturel
- Messages: 14
- Enregistré le: 28 Sep 2015, 21:10
-
 par rudy196 » 30 Sep 2015, 17:48
par rudy196 » 30 Sep 2015, 17:48
zygomatique a écrit:je t'ai dit comment à 20h09 .... par récurrence ...
Bh j'ecris l'égalité

p^n+1 +µ(1-p)^n+1+;)p^n +µ(1-p)^n =;)p^n+2 +µ(1-p)^n+2
Mais je n'arrive pas à tranformer la premier partie de l'équation en la deuxieme
Je comprend pas pourquoi on utiliserai la récurrence

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 30 Sep 2015, 18:23
par zygomatique » 30 Sep 2015, 18:23
l'égalité est ce qu'on veut !!!
donc non on ne l'écrit pas !!!
on part du membre de droite et on arrive au membre de gauche .....
il suffit de factoriser convenablement ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
rudy196
- Membre Naturel
- Messages: 14
- Enregistré le: 28 Sep 2015, 21:10
-
 par rudy196 » 30 Sep 2015, 18:48
par rudy196 » 30 Sep 2015, 18:48
j'ai factoriser du mieux que je pouvais vraiment mais je suis arriver a : p^(n)(2;)+1)+(µ(1-p)^(n))(1-p) =

p^n+2 +µ(1-p)^n+2
a partir de la je sais vraiment plus quoi faire

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 30 Sep 2015, 19:22
par zygomatique » 30 Sep 2015, 19:22
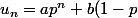^n)
où p est le nombre d'or ...
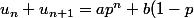^n + ap^{n + 1} + b(1 - p)^{n + 1} = ap^n(1 + p) + b(1 - p)^n(2 - p) = ap^np^2 + b(1 - p)^n(1 - p)^2 = ap^{n + 2} + b(1 - p)^{n + 2} = u_{n + 2})
:zen:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
rudy196
- Membre Naturel
- Messages: 14
- Enregistré le: 28 Sep 2015, 21:10
-
 par rudy196 » 30 Sep 2015, 19:45
par rudy196 » 30 Sep 2015, 19:45
Ah merci beaucoup mon erreur vennais de quand j'ai factoriser ap^n car jai oublier que p était a la puissance 0 donc 1 et j'ai pas penser a rassembler les n et les ² pour former les n+2 merci
Cependant il me reste encore deux question ...
Réciproquement démontrez que pour toute suite u de E il existe 2 réels a et b tel que
Un = ap^n+b(1-p)^2
Je dois suivre quelle démarche pour trouver vue qu'on utilise pas la meme méthode

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 01 Oct 2015, 16:53
par zygomatique » 01 Oct 2015, 16:53
les réels a et b sont déterminés par les deux premiers termes de la suite ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 195 invités
