Gros problème de TS!!!!

[lili28]

g un petit problème.. g un DM et je n' arrive pas à réaliser le 2ème exo:

Résoudre ds R l'équation :

1+(x+1)/(x-1)+[x+1/x-1]au carré+[x+1/x-1]au cube=0


avec b=(x+1)/(x-1)

voilà ca serait super sympa si vous pouviez m'aider d'autant plus que je dois le rendre lundi un gros merci d'avance :we:

[Alpha]

Salut,

en posant égal à ce qui t'es indiqué,

ton équation devient .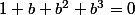

L'idée est alors de résoudre cette équation, puis, une fois les différentes valeurs possibles de b trouvées (notées ,,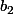 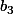(s'il y en a 3)), résoudre 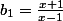, idem pour 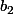et .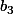

Comment résoudre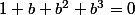 ? Cette équation a une racine évidente (essaye de voir si 0,1 ou -1 est solution par exemple).

Bon courage.

[Anonyme]

Pour b différent de 1 on a : 1+b+b^2+b^3=(1-b^4)/(1-b)

(voir chapitre suites géométriques)

[Anonyme]

Pardon je n'avais pas vu qu'une réponse avait déjà été donnée.

[Anonyme]

ok merci bcp mais cmt prouver que 1 et -1 sont des racines évidentes? par déduction ? de plus cmt résoudre 1=x+1/x-1 ainsi que -1=x+1/x-1

Je vs remercie encore

[Anonyme]

Pour prouver les racines evidentes, il te suffit de remplacer b par leur valeur et de montrer qu'elles sont effectivement solutions de l'équation
Ensuite pour resoudre les 2 ptites équations, c'est tout simple
1=x+1/x-1 équivaut à x-1=x+1 donc il n'y a aucune solution

-1=x+1/x-1 équivaut à x+1=1-x soit x=0

[Alpha]

Oui, j'ai fait une petite erreur suite au message de non inscrit, 1 n'est pas solution évidemment.

Mais -1 l'est. Pour s'en rendre compte, il suffit de remplacer dans l'équation b par -1.

Ensuite, 1+ b+b²+b^3 = 0 devient (b+1) (ab² +cb + d) = 0.

Il te reste à trouver le trinôme du second degré correspondant.

(b+1) (ab² +cb + d) = ab^3 + cb²+ bd + ab² +cb +d = 1+ b+b²+b^3,

Il te reste à identifier les coefficients.

En fait on se rend compte que 1+ b+b²+b^3 = (b+1)(b²+1).

Par conséquent, -1 est l'unique racine de l'équation, car b²+1=0 n'a pas de racines dans R.