Gros probleme!
13 messages
- Page 1 sur 1
Gros probleme!
Bonour!Voici un exercice que je n'arrive pas a faire alors que ca fais plus de deux heures que j'essaye:
2 2
1)Développer (x + 3x+ 1)
2)Montrer sur trois exemples que le produit des quatre entiers naturels consécutifs augmenté de 1 est le carré d'un entier naturel
3)PROUVER LE CAS PRECEDENT DANS LE CAS GENERAL
Je ne vois aps du tout comment on peut faire le 3!
2 2
1)Développer (x + 3x+ 1)
2)Montrer sur trois exemples que le produit des quatre entiers naturels consécutifs augmenté de 1 est le carré d'un entier naturel
3)PROUVER LE CAS PRECEDENT DANS LE CAS GENERAL
Je ne vois aps du tout comment on peut faire le 3!
oui mais...
En effet,vous avez raison mais quand vous ecrivez que
je ne comprends pas pourquoi
TEX](k^2+3k+2)=(k+1)(k+2)[/TEX] c'est touvable
donc
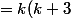(k+1)(k+2)+1)
gol_di_grosso a écrit:a=k(k+3) b=1
ça va là ?
bon après tu factorise pas k(k+3)
ensuitec'est touvable
donc
donc
je ne comprends pas pourquoi
TEX](k^2+3k+2)=(k+1)(k+2)[/TEX] c'est touvable
donc
on part de (k(k+3)+1)² =(k²+3k+1)² si tu préfère
après quelque ligne de calcule :
=k(k+3)(k²+3k+2)+1 or k²+3k+2 = (k+1)(k+2) (fais le calcule)
donc
=k(k+3)(k+2)(k+1)+1
=(k+3)(k+2)(k+1)k+1
donc
k(k+3)(k+2)(k+1)+1=(k²+3k+1)²
ainsi le produit de trois entiers sonsécutif augmenté de un c'est égal à (k²+3k+1)² qui est le carré d'un nombre entier (l'entier c'est k²+3k+1)
après quelque ligne de calcule :
=k(k+3)(k²+3k+2)+1 or k²+3k+2 = (k+1)(k+2) (fais le calcule)
donc
=k(k+3)(k+2)(k+1)+1
=(k+3)(k+2)(k+1)k+1
donc
k(k+3)(k+2)(k+1)+1=(k²+3k+1)²
ainsi le produit de trois entiers sonsécutif augmenté de un c'est égal à (k²+3k+1)² qui est le carré d'un nombre entier (l'entier c'est k²+3k+1)
k(k+3)(k+2)(k+1)+1=
k au carré+3k+k au carré+2k+k au carré+k=
6k+k exposant 4
ce qui n'est pas egal a :
En effet,je ne comprends pas vous mettez
(k²+3k+1)²,ce qui fait
(k au carré+3k+1)(k au carré+3k+1)
Donc,(k au carré+3k+1)(k au carré+3k+1) serait égal a k(k+3)(k+2)(k+1)+1??
Pourquoi??(ahhh je ne comprends plus^^) :mur:
k au carré+3k+k au carré+2k+k au carré+k=
6k+k exposant 4
ce qui n'est pas egal a :
En effet,je ne comprends pas vous mettez
(k²+3k+1)²,ce qui fait
(k au carré+3k+1)(k au carré+3k+1)
Donc,(k au carré+3k+1)(k au carré+3k+1) serait égal a k(k+3)(k+2)(k+1)+1??
Pourquoi??(ahhh je ne comprends plus^^) :mur:
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

