Bonjour, j'ai besoin de votre aide pour traiter cet exo:
ABCD est un quadrilatère convexe.
soit E un point [AB] et F un point de [AD] tels que AE/AB = AF/AD.
La droite (D1), parallèle à (BC) passant par E et la droite (D2), parallèle à (CD) passant par F se coupent en un point O.
Démontrer que les points A, O et C sont alignés.
Géometrie
4 messages
- Page 1 sur 1
Re: Géometrie
Salut,
36000 façon de procéder plus ou moins rapide et dépendant de ce qu'on connaît et de ce qu'on accepte d'utiliser comme outil.
Parmi les plus rapides et basique (niveau collège) qui me vienne à l'esprit, il y a sans doute ça :
C'est quoi l'image des points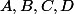 par l'homothétie de centre
par l'homothétie de centre  et de rapport
et de rapport 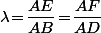 ?
?
36000 façon de procéder plus ou moins rapide et dépendant de ce qu'on connaît et de ce qu'on accepte d'utiliser comme outil.
Parmi les plus rapides et basique (niveau collège) qui me vienne à l'esprit, il y a sans doute ça :
C'est quoi l'image des points
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Géometrie
je vois l'idée, utiliser la conservation de l'alignement par l’homothétie. mais je bloque sur l'image du point C par h.
on a:
- h(A) = A
- h(B) = E
- h(D) = F
mais h(C) je suppose que ca va donner O mais je ne sais pas pourquoi?
on a:
- h(A) = A
- h(B) = E
- h(D) = F
mais h(C) je suppose que ca va donner O mais je ne sais pas pourquoi?
Re: Géometrie
Une autre idée (si tu as vu les vecteurs) : Il existe un réel  tel que
tel que 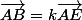 et
et 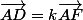 .
.
Il existe un point sur
sur ) tel que
tel que 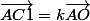 , et
, et  sur
sur ) tel que
tel que 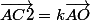 . Je te laisse conclure.
. Je te laisse conclure.
Pour l'homothétie, tu peux déterminer l'image de la droite (BC) et celle de la droite (AD), puis l'image de leur point d'intersection.
Il existe un point
Pour l'homothétie, tu peux déterminer l'image de la droite (BC) et celle de la droite (AD), puis l'image de leur point d'intersection.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 93 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
