Bonjour, j'ai un petit problème concernant un exercice de géométrie.
Je dois trouver le lieu géométrique décrit par un point.
J'ai inséré 2 photos (un original et l'autre avec quelques repères.
1 er lien : https://i.postimg.cc/WbJGXgbM/C5-C6929- ... 183-B6.jpg
2 eme lien : https://i.postimg.cc/qqVYKhLy/Devoir-Math-2.jpg
Le point F est le point B lorsqu'il rencontre l'axe y=2 et le point E est le point A lorsqu'il rencontre l'axe y=2
sachant que la porte mesure 2m, j'ai comme coordonnées:
A(1/2, 2) D(0,2) E(1,2) F(-1,2)
PS : Le point F est le point B lorsqu'il rencontre l'axe y=2 et le point E est le point A lorsqu'il rencontre l'axe y=2
Comme on ne peut pas déterminer l'ordonnée de B, je place λ pour son ordonnée donc B(-1/2, λ)
Je cherche l'équation de la droite a= IABI.
a=> y= (-2x-1+4λ²)/4λ
Je cherche également l'équation de b = IFBI
b=> y=(-x-9+4λ)/2λ-4
C'est bon jusqu'ici ou je me suis embrouillé avec le λ et l'équation des droites?
A partir de ces données, je ne sais toujours pas comment je peux trouver le lieu décrit par le point B...
Les exercices que nous avons faits consistaient à trouver un lieu d'un point qui était l'intersection de plusieurs droites or là ce n'est pas le cas... Nous avons vu la méthode des génératrices et de traduction mais je ne vois pas comment l'appliquer ici...
Pouvez vous m'aider?
Merci d'avance
Géométrie (lieu géométrique) (niveau lycée)
12 messages
- Page 1 sur 1
Re: Géométrie (lieu géométrique) (niveau lycée)
Bonjour
un indice
On peut remarquer que [AM]+[MD]=[AP]
À partir de là on a tout (au niveau collège en tout cas)
un indice
On peut remarquer que [AM]+[MD]=[AP]
À partir de là on a tout (au niveau collège en tout cas)
Re: Géométrie (lieu géométrique) (niveau lycée)
Merci de votre réponse rapide
Oui effectivement mais je ne comprends pas en quoi ça pourrait m'aider sachant que je dois trouver la courbe que décrit le point B ?(et le point P se déplaçant verticalement)
Oui effectivement mais je ne comprends pas en quoi ça pourrait m'aider sachant que je dois trouver la courbe que décrit le point B ?(et le point P se déplaçant verticalement)
Re: Géométrie (lieu géométrique) (niveau lycée)
Wolfchess a écrit:Merci de votre réponse rapide
Oui effectivement mais je ne comprends pas en quoi ça pourrait m'aider sachant que je dois trouver la courbe que décrit le point B ?(et le point P se déplaçant verticalement)
vous dites oui effectivement (bah alors il fallait déjà que ce soit vous qui le disiez et non moi) et si je donne la réponse à la question vous direz oui effectivement mais sans dire en quoi ça va m'aider pour la réponse vu que je vous aurai donné la réponse
oui effectivement c'est du niveau collège et non du niveau lycée : oui effectivement
avec des effectivement on arrête les guerres dans le monde ; effectivement la paix est la solution à la guerre
Re: Géométrie (lieu géométrique) (niveau lycée)
Je suggère de prendre l'origine du repère en D, avec toujours l'axe des abscisses horizontal et celui des ordonnées vertical.
On note (x,y) les coordonnées de B dans ce repère orthonormé.
Le point A se promène sur l'axe des abscisses.
On exprime que le milieu P de AB est sur l'axe des ordonnées (ça nous donne l'abscisse de A) et que la distance AB est fixe, égale à 2.
On obtient ainsi assez immédiatement l'équation de la courbe ou se promène A.
On note (x,y) les coordonnées de B dans ce repère orthonormé.
Le point A se promène sur l'axe des abscisses.
On exprime que le milieu P de AB est sur l'axe des ordonnées (ça nous donne l'abscisse de A) et que la distance AB est fixe, égale à 2.
On obtient ainsi assez immédiatement l'équation de la courbe ou se promène A.
Re: Géométrie (lieu géométrique) (niveau lycée)
Quand j'étais au lycée, mon prof de maths nous avait montré un "ellipsographe d'Archimède" en bois, de ce genre :

emprunté à Wikimedia .Par Zephyris — Travail personnel, CC BY-SA 3.0,
C'était il y a 45 ans ....

emprunté à Wikimedia .Par Zephyris — Travail personnel, CC BY-SA 3.0,
C'était il y a 45 ans ....
Re: Géométrie (lieu géométrique) (niveau lycée)
Bonjour
On va garder ton repère
Les coordonnées de D sont donc D=(0,2) de A:) avec
avec  et
et
.)
L'ingrédient essentiel est que distance(A,P)=cste=1 .
Or^2=1) , un calcul rapide donne
, un calcul rapide donne

Doù)
Posons (x,y) les coordonnées de B (avec x=-X_A\in [-1,0])
On a^2=1)
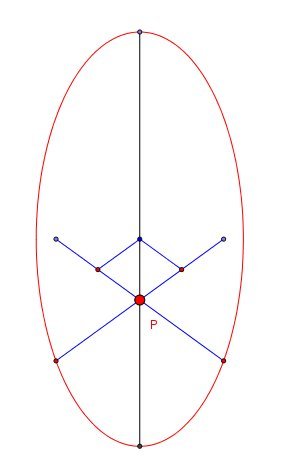
On reconnait l'équation d'une ellipse de centre D(0,2) dont les demi-axes sont de longueur 2 et 1.
B parcourant 1/4 de cette ellipse comme on le voit sur le dessin de @chan
On va garder ton repère
Les coordonnées de D sont donc D=(0,2) de A:
L'ingrédient essentiel est que distance(A,P)=cste=1 .
Or
Doù
Posons (x,y) les coordonnées de B (avec x=-X_A\in [-1,0])
On a
On reconnait l'équation d'une ellipse de centre D(0,2) dont les demi-axes sont de longueur 2 et 1.
B parcourant 1/4 de cette ellipse comme on le voit sur le dessin de @chan
Re: Géométrie (lieu géométrique) (niveau lycée)
Pourquoi faire l'exercice à la place de Wolfchess ?
Puisque aviateur a spoilé le truc, je me permets d'indiquer une variante, suivant les indications que j'avais données (avec D l'origine du repère et) les coordonnées de B dans ce repère) :
les coordonnées de B dans ce repère) :
Les coordonnées de A sont) puisque A est sur l'axe des abscisses et que le milieu de A et B est sur l'axe des ordonnées. On écrit que la distance de A à B est 2 :
puisque A est sur l'axe des abscisses et que le milieu de A et B est sur l'axe des ordonnées. On écrit que la distance de A à B est 2 :
)^2+ (y-0)^2=4x^2 +y^2\;) .
.
C'est tout.
Puisque aviateur a spoilé le truc, je me permets d'indiquer une variante, suivant les indications que j'avais données (avec D l'origine du repère et
Les coordonnées de A sont
C'est tout.
Re: Géométrie (lieu géométrique) (niveau lycée)
Ah, au fait, aviateur, une petite coquille : les coordonnées de A, dans le repère dans lequel tu travailles, sont ) et pas
et pas ) . Il faut croire que tu avais tout de même envie que A se promène sur l'axe des abscisses.
. Il faut croire que tu avais tout de même envie que A se promène sur l'axe des abscisses. 
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :