Le Sujet: ABCDH est une pyramide de base le rectangle ABCD avec AB=6cm, BC=4 cm et de hauteur DH= 3cm.
1) Faire une figure en perspective cavaliere avec un angle de fuite de 45° et un facteur de report de 0.5
2) Quel est le volume de la pyramide ABCDH?
3) M est un point de segment [HC] tel que HM=5/8HC et N un point du segment [BH] tel que HN=5/8HB
a) Montrer que les droites (AD) et (MN) sont paralleles.
b) Expliquer pourquoi les droites (AN) et (DM) sont sécantes. On appelle P leur point d'intersection.
C) Quelle est l'intersection des plans (HAB) et (HDC)? Justifier
D) Que peut-on dire des droites (AB), (CD) et (HP)? Justifier
Reponse:
1)
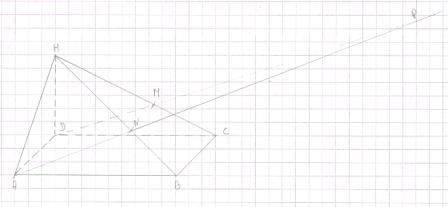
2) Vabcdh= aire de la base x hauteur x 1/3
= 24 cm3
3)
a) J'ai utiliser le thereme du toit:
# (ADN) et (BCM) se coupent en (MN)
# (AD) et (CB) sont paralleles
PAr le thereome du toit, on en deduit que (Ad) et MN) sont paralleles
b) Je ne sais pas comment demontrer si vous pouver m'aider serait un coup de main pour mon dm.
Merci
