Je galère trop en maths : DM

[Anonyme]

bonjour je suis en 1ère S et là je galère trop sur le boulot que j'ai à faire :

la fonction u est définie sur [0;4], croissante sur [0;2] et décroissante sur [2;4]

1° construire la représentation graphique de la fonction v défnie sur [0;4] par v(x) = - x + 4 bon j'ai pris des valeurs et ça donne une courbe décroissante sur [0;4]

2° sur quel intervalle est-on certain du sens de variation de la fonction u+v
sur [2;4] car les 2 sont décroissante sur ces 2 intervalles

mais la question suivante me pose problème :
3° construire point par point la réprésentation graphique de la fonction u+v je ne vois pas du tout comment faire sachant qu'on ne sait pas à combien est égale la fonction u

merci de m'aider je vous demanderez peut-être d'autres chose car j'ai beaucoup de mal à faire mes exercices.

[Marrynn]

voila je me suis inscrite maintenant!

[Chimerade]

bonjour je suis en 1ère S et là je galère trop sur le boulot que j'ai à faire :

la fonction u est définie sur [0;4], croissante sur [0;2] et décroissante sur [2;4]

1° construire la représentation graphique de la fonction v défnie sur [0;4] par v(x) = - x + 4 bon j'ai pris des valeurs et ça donne une courbe décroissante sur [0;4]

2° sur quel intervalle est-on certain du sens de variation de la fonction u+v
sur [2;4] car les 2 sont décroissante sur ces 2 intervalles

mais la question suivante me pose problème :
3° construire point par point la réprésentation graphique de la fonction u+v je ne vois pas du tout comment faire sachant qu'on ne sait pas à combien est égale la fonction u

merci de m'aider je vous demanderez peut-être d'autres chose car j'ai beaucoup de mal à faire mes exercices.

Exact ! Cela veut dire qu'il te faut choisir toi-même une fonction qui a ces propriétés. Que dirais-tu de u(x)=4-(x-2)² ?

[phenomene]

Bonjour, une remarque sur le fonction : c'est une fonction affine, donc sa représentation graphique est une droite ! Il suffit donc de deux points pour la tracer.

Quant à tracer la représentation graphique de , c'est en effet impossible sans rien savoir sur ; es-tu sûre de ton énoncé ?

[Marrynn]

oui je suis certaine de mon énoncé c'est écrit noir sur blanc j'ai juste omis de vous mettre la représentation graphique de u mais elle ne nous apporte rien de plus car c'est une simple courbe coirssante jusqu'à 2 et décroissante jusqu'à 0.

[phenomene]

Mais si elle apporte quelque chose en plus ! Tu as tout ce qu'il faut maintenant. Je suppose que tu as vu en cours comment obtenir la représentation graphique de 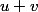à partir de celles de et , non? Sinon, je te dis comment faire : l'ordonnée du point d'abscisse de la représentation graphique de 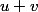est , c'est-à-dire la somme des ordonnées des points d'abscisse des représentations graphiques de et de ( et respectivement), que tu peux lire sur la figure.

[Marrynn]

merci bcp je n'avais pas du tou vu ça en cours.
j'ai un pb aussi c'est que je connais les réponses ms je ne sais pas justifier :
donner le sens de variation de u(x)=x et v(x) = x - 4 sur R+ je sais qu'elles sont croissantes sur R+ mais comment justifier?