Fractions avec racines carrées a démontrer
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
 par angelique2605 » 04 Sep 2016, 15:52
par angelique2605 » 04 Sep 2016, 15:52
Bonjour, je reviens vers vous car j'ai une fraction assez complexe où il faut démontrer que pour tous nombres a et b strictement positifs tels que a≠b, on a :

je ne sais pas du tout par ou commencer pour démontrer cela, pourriez vous me donner un coup de pouce ?
je précise que les "V" sont des racines carrées que je n'ai pas réussi a faire

merci par avance!

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 04 Sep 2016, 15:54
par Lostounet » 04 Sep 2016, 15:54
angelique2605 a écrit:Bonjour, je reviens vers vous car j'ai une fraction assez complexe où il faut démontrer que pour tous nombres a et b strictement positifs tels que a≠b, on a :

je ne sais pas du tout par ou commencer pour démontrer cela, pourriez vous me donner un coup de pouce ?
je précise que les "V" sont des racines carrées que je n'ai pas réussi a faire

merci par avance!
Dans la fraction initiale, multiplie en haut et en bas par le nombre √a - √b
Puis utilise le fait que
( u - v) = u^2 - v^2)
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 04 Sep 2016, 17:27
par Razes » 04 Sep 2016, 17:27
pose
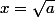
et

afin d'alléger l'écriture. Utilise les identités remarquables.
-
triumph59
- Membre Rationnel
- Messages: 643
- Enregistré le: 16 Mar 2013, 16:49
-
 par triumph59 » 04 Sep 2016, 17:43
par triumph59 » 04 Sep 2016, 17:43
Bonsoir, tu peux également vérifier que le produit en croix appliqué aux 2 fractions est égal : le produit du numérateur de la première fraction par le dénominateur de la seconde est-il égal au produit du numérateur de la seconde fraction par le dénominateur de la première ?
Si oui les 2 fractions sont égales, sinon elles ne le sont pas

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 04 Sep 2016, 18:24
par zygomatique » 04 Sep 2016, 18:24
salut
puisque a et b sont positifs et
si on connaît ses identités remarquables et la définition de la racine carrée d'un nombre alors :
1/ tout nombre positif est le carré de sa racine carrée
2/
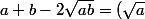^2 - 2 \sqrt a \sqrt b + (\sqrt b)^2 = ...)
3/
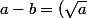^2 - (\sqrt b)^2 = ...)
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 270 invités
