Formules difficiles

[Soch]

Bonjour, j'ai cet exercice à faire mais je ne vois pas du tout comment démontrer, je ne sais pas du tout à quoi serve ces formules, quelqu'un pourrait-il m'aider ?

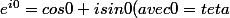J'ai trouver que mais je vois pas comment l'utiliser ?

[mathelot]

en conjuguant







(1)

cette formule permet de calculer le module de (1)

[Soch]

Merci beaucoup de votre réponse mais pour démontrer les deux premieres formules est- ce que j'ai le droit d'utiliser et directement ?

[mathelot]

bah oui. je ne pense pas que cela serve mais tes deux égalités sont valides toutefois.

[mathelot]

ces formules proviennent de la série



le produit de Cauchy, produit de convolution, donne



quand on se restreint à l'axe des imaginaires


et , il ne reste plus qu'à montrer que l'application est une surjection "au dessus" du cercle trigonométrique.

cf , entre autres, Lang "analyse" et H.Cartan "théorie élémentaire des fonctions analytiques"

[Soch]

Je n'arrive pas à démontrer les formules de et je ne vois pas quoi utiliser ? De quelle formule je dois partir au départ ?
Et pour l'expression du sinus, je remplace par ?

[Soch]

Je ne sais pas ce qu'est une surjection désolé

[mathelot]

Je n'arrive pas à démontrer les formules de et je ne vois pas quoi utiliser ? De quelle formule je dois partir au départ ?
Et pour l'expression du sinus, je remplace par ?

en Terminale, il s'agit d'admettre la définition suivante


après tes connaissance en trigo et nbres complexes te mènent plus ou moins loin.

Il vient notamment
et

Et pour l'expression du sinus, je remplace par ?

oui.

[Soch]

Je n'ai pas encore commencé la trigonométrie en cours mais on a fait les nombres complexes, je vais regarder le cours dans mon livre, merci