bonsoir
je me présente à vous avec un léger soucis mathématique
je m'explique je cherche a extraire y de la formule si dessous
a=xy+(25(y-1)y
a et x sont des valeurs connue j'aimerais que a la fin je n'est que y d'un cote et les valeur connue de l'autre
pour pouvoir les rentrer dans un tableur et que la formule me sorte y = ......
merci est bonne soirée
ps :
je tient a précisé que j'ai poster dans cette section car cela ressemble plus a un niveau lycée mais cela fait bien longtemps que j'ai quitté l'école
pour expliquer le problème
je suis partit d'un système d'achat d'un objet qui augment sont prix automatiquement de 50 a chaque fois que l'on en acheté 1
se qui fait
prix 1 50
prix 2 100
prix 3 150
etc
et je voulais donc savoir combien l'on dépenser pour l'achat de 10 objets par exemple
donc j'ai trouver la formule a=xy+(25(y-1)y
ou "a" et la somme total dépensé
x le prix du premier objet que l'on achète
et y le nombre d'objet que l'on veut acheter
maintenant je recherche a faire l'inverse j'ai 1000 a dépenser combien je peux avoir d'objets
si cela peux aidé dans le raisonnement
Formule a 1 inconue
11 messages
- Page 1 sur 1
Bonjour,
Il me semble que vous soyez dans un cas pratique, alors je vais vous épargner les détails. Néanmoins si vous tenez à connaître la méthode que j'ai utilisée, ne manquez pas de me la demander. En gardant votre notation, on obtient :
+\sqrt{(\frac{x}{25}-1)^2+\frac{4a}{25}}}{2})
Toutefois, dans votre cas où x=50 et l'augmentation est également 50 ; il est plus simple de poser :
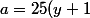y)
De façon que :
^2+\frac{4a}{25}}}{2})
En espérant vous avoir aidé. :++:
Il me semble que vous soyez dans un cas pratique, alors je vais vous épargner les détails. Néanmoins si vous tenez à connaître la méthode que j'ai utilisée, ne manquez pas de me la demander. En gardant votre notation, on obtient :
Toutefois, dans votre cas où x=50 et l'augmentation est également 50 ; il est plus simple de poser :
De façon que :
En espérant vous avoir aidé. :++:
bjr
je me demandais si tu avais bien posé ta formule, ce que je comprends
prix du 1er achat=50
prix 2è achat=2x50
prix 3è achat=3x50
prix nè achat=nx50
la somme totale depensée=S= 50(1+2+3..+n)=50(n)(n+1)/2=25n(n+1)=S
pour l'achat de 10 objets on a S=25(10)(11)=2750
à l'inverse on connait S=1000
1000=25n(n+1) à resoudre
40=n²+n
soit n²+n-40=0 que tu dois savoir resoudre
je me demandais si tu avais bien posé ta formule, ce que je comprends
prix du 1er achat=50
prix 2è achat=2x50
prix 3è achat=3x50
prix nè achat=nx50
la somme totale depensée=S= 50(1+2+3..+n)=50(n)(n+1)/2=25n(n+1)=S
pour l'achat de 10 objets on a S=25(10)(11)=2750
à l'inverse on connait S=1000
1000=25n(n+1) à resoudre
40=n²+n
soit n²+n-40=0 que tu dois savoir resoudre
bonjour
ma formule
1: 50
2: 50+100
3: 50+100+150
4: 50+100+150+200
etc
ma formule et juste et celle de dude et exact aussi pour le calcule de y
le probleme qu ise passe avec votre formule c'est que si je ne commence pas au premiere achat mais au 10 eme
exemple
10: 500
11: 500+550
12: 500+550+600
etc
et que je veut juste acheter 3 points cela va me couté 1650 alors que avec votre formule je doit repartir du premier achat
je ne sait pas si je me fait bien comprendre
ma formule
1: 50
2: 50+100
3: 50+100+150
4: 50+100+150+200
etc
ma formule et juste et celle de dude et exact aussi pour le calcule de y
le probleme qu ise passe avec votre formule c'est que si je ne commence pas au premiere achat mais au 10 eme
exemple
10: 500
11: 500+550
12: 500+550+600
etc
et que je veut juste acheter 3 points cela va me couté 1650 alors que avec votre formule je doit repartir du premier achat
je ne sait pas si je me fait bien comprendre
rikimaruneo a écrit:merci de votre réponse rapide
la première formule fonctionne parfaitement
mais j aimerais avoir le détail si cela ne vous dérange pas
pour la second il manque x a prendre en compte a chaque nouvelle achat
mais merci beaucoup
Tout à fait,
Pour ce qui est des détails :
A ce moment, la méthode mathématique qui permet d'avoir les valeurs de l'inconnue y se présente comme suit :
a étant positive ;
Comme y est positive, on prendra alors la valeur de y qui est positive:
Voici un lien qui présente la forme générale de cette méthode, si ça vous intéresse : http://www.mathematiquesfaciles.com/equations-equation-du-second-degre_2_33929.htm
:++:
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
