Formule du binôme de Newton

[rb90]

Bonjour
Je ne comprend pas la Formule du binôme de Newton :mur: j'ai essayé de trouver des astuces, mais après la puissance 3 je suis perdu, pourquoi pour la puissance 4 les coef sont 1 4 6 4 1.

Merci a vous.

[Micki28]

Bonjour,

Voici la formule du binôme de Newton:



Qu'est ce que tu ne comprends pas?

Peut-être le: ?

Pour n = 4, on aura les 4 coefficients suivant:



Voilà...

[vincentroumezy]

Pour calculer les coefficients, tu as une formule explicite dans ton cours de TS, sinon, faos le triangle de Pascal?

[rb90]

Je ne comprend pas cette forme,
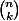ça vient du triangle de pascal ça ?
mais comment on trouve 1 4 6 4 1 ? avec le triangle je comprend mais si il faut faire un triangle a chaque fois c'est pas pratique.

Si je pose pour avec la formule j'arrive a :
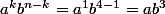mais je ne trouve pas 4.


désolé je viens d'un Bac Sti de 2008, je me remet a niveau en math pour septembre (reprise d'étude). :help:

[MacManus]

Je ne comprend pas cette forme,
ça vient du triangle de pascal ça ?
mais comment on trouve 1 4 6 4 1 ? avec le triangle je comprend mais si il faut faire un triangle a chaque fois c'est pas pratique.

Si je pose pour avec la formule j'arrive a :
mais je ne trouve pas 4.


désolé je viens d'un Bac Sti de 2008, je me remet a niveau en math pour septembre (reprise d'étude). :help:

En fait on a

avec et par convention.

par exemple:
correspond au premier coefficient dans le développement de

[MacManus]

Pour n=4 (c'est-à-dire la 5ème ligne du triangle de Pascal), on peut écrire explicitement la somme:

[rb90]

Elle vient d'ou cette formule ? elle a un nom ?
ça ressemble beaucoup a la formule de la combinaison en Probabilité sauf que l'on aurait mis k! au numérateur, n!(k-p)! au dénominateur. Je dis peut etre une connerie

merci beaucoup de votre aide, MacManus et vincentroumezy

[vincentroumezy]

Cette formule, c'est LA formule de définition, et bien sûr que ça ressemble à une combinaison, C'EST la combinaison de k parmi n.

[rb90]

Ok merci
vous êtes trop fort !!!