Former équation un plan // droite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
mythos75
- Membre Naturel
- Messages: 35
- Enregistré le: 11 Aoû 2008, 15:34
-
 par mythos75 » 29 Aoû 2008, 16:09
par mythos75 » 29 Aoû 2008, 16:09
Bonjour,
J'ai besoin de votre aide côté géo

L'énoncé :
Formez l'équation du plan a qui passe par le point M (1,2,-3) et qui est parallèle aux droites :
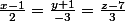
et 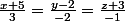
Si je comprends bien : pour un parallélisme entre un plan et des droites il faut que le produit scalaire du vecteur normal du plan avec ceux des vecteurs directeurs des droites soit = 0 ?
Je n'y arrive pas, pouvez-vous m'indiquer la marche à suivre svp ?

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 29 Aoû 2008, 19:45
par Sa Majesté » 29 Aoû 2008, 19:45
Oui c'est ça
Commence par déterminer un vecteur directeur de chacune des 2 droites
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 29 Aoû 2008, 19:48
par XENSECP » 29 Aoû 2008, 19:48
Moi je réécrirais simplement les 2 droites sous forme paramétrée... et là le vecteur directeur apparaît tout de suite ^^
Déjà fait ca ;)
-
mythos75
- Membre Naturel
- Messages: 35
- Enregistré le: 11 Aoû 2008, 15:34
-
 par mythos75 » 30 Aoû 2008, 12:11
par mythos75 » 30 Aoû 2008, 12:11
V. directeur 1 : (2, -3, 3) ?
V. directeur 2 : (3, -2, -1) ?
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 30 Aoû 2008, 12:24
par Euler911 » 30 Aoû 2008, 12:24
Bonjour,
Pour

j'ai (2,-3,3)
Mon système d'équations paramétrée est le suivant:
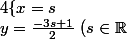\\z=\frac{3s+11}{2})
EDIT: C'est bon : j'ai fait une erreur en recopiant
)
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 30 Aoû 2008, 12:29
par Euler911 » 30 Aoû 2008, 12:29
Ok pour

-
mythos75
- Membre Naturel
- Messages: 35
- Enregistré le: 11 Aoû 2008, 15:34
-
 par mythos75 » 30 Aoû 2008, 12:32
par mythos75 » 30 Aoû 2008, 12:32
Ok merci ;
Mais comment à présent trouver le v. normal ?
Il faut que (2*?) + (-3*?) + (3*?) = 0
ET QUE :
(3*?) + (-2*?) + (-1*?) = 0
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 30 Aoû 2008, 12:36
par Euler911 » 30 Aoû 2008, 12:36
Un plan est formé par deux vecteurs directeurs non // est-ce que (3,-2,-1) et (2,-3,3) sont multiples???
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 30 Aoû 2008, 12:39
par XENSECP » 30 Aoû 2008, 12:39
Hum en fait...le vecteur normal au plan c'est simplement le produit vectoriel des 2 vecteurs directeurs des droites ;)
Parce que le vecteur produit vectoriel est orthogonal aux 2 vecteurs directeurs de droites (démonstration facile si tu connais le produit vectoriel), et donc tu as a,b,c dans :
ax+by+cz+=0
Et puis tu conclus avec le fait que M appartienne au plan ;)
-
mythos75
- Membre Naturel
- Messages: 35
- Enregistré le: 11 Aoû 2008, 15:34
-
 par mythos75 » 30 Aoû 2008, 12:46
par mythos75 » 30 Aoû 2008, 12:46
Euh qu'est-ce que le produit vectoriel ?
On fait (2*3)x+(-3*-2)y+... ?
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 30 Aoû 2008, 12:48
par Euler911 » 30 Aoû 2008, 12:48
On ne voit pas le produit vectoriel en Belgique! Donc suis les indices de mon dernier poste!
-
mythos75
- Membre Naturel
- Messages: 35
- Enregistré le: 11 Aoû 2008, 15:34
-
 par mythos75 » 30 Aoû 2008, 12:54
par mythos75 » 30 Aoû 2008, 12:54
Euler911 a écrit:Un plan est formé par deux vecteurs directeurs non // est-ce que (3,-2,-1) et (2,-3,3) sont multiples???
Non, donc pas //, donc on a les deux v. directeurs, donc...
OM (1 ,2, -3)
MB (2,-4,-4)
MC (1,-5,0)
Eq. param. : ?
x = 1 + 2r +s
y = 2 - 4r -5s
z = -3 - 4r
Edit : je crois que j'ai fait un truc à la rien à voir... on veut que le plan soit // aux droites...
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 30 Aoû 2008, 12:58
par Euler911 » 30 Aoû 2008, 12:58
D'ou sortent O, B et C???
Le système d'équations paramétriques d'un plan dont les vecteurs directeurs sont u et v et contenant le point M est:
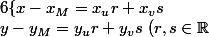\\z-z_M=z_u r+z_v s)
-
mythos75
- Membre Naturel
- Messages: 35
- Enregistré le: 11 Aoû 2008, 15:34
-
 par mythos75 » 30 Aoû 2008, 13:01
par mythos75 » 30 Aoû 2008, 13:01
Euh j'ai voulu refaire des vecteurs avec des vecteurs je pense...
Eq. param. : ?
x = 1 + 2r + 3s
y = 2 - 3r -2s
z = -3 + 3r -s
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 30 Aoû 2008, 13:03
par Euler911 » 30 Aoû 2008, 13:03
Voilà c'est fait! Parfait.
-
mythos75
- Membre Naturel
- Messages: 35
- Enregistré le: 11 Aoû 2008, 15:34
-
 par mythos75 » 30 Aoû 2008, 13:05
par mythos75 » 30 Aoû 2008, 13:05
Ok c'était vraiment tout bête en fait :zen:
Merci compatriote.
-
mythos75
- Membre Naturel
- Messages: 35
- Enregistré le: 11 Aoû 2008, 15:34
-
 par mythos75 » 30 Aoû 2008, 13:10
par mythos75 » 30 Aoû 2008, 13:10
Si quelqu'un a le courage de continuer à me supporter, exercice suivant :
Ecrire l'équation de la droite passant par les points A (-1,2,3) et B (0,4,-1). Le point C (-3,0,6) et les points A et B sont-ils alignés ? Expliquer par un calcul.
V. directeur = (-1, 2, -4)
Eq. de la droite : ?
x = -1
y = 2 + 4k
z = 3 - k
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 30 Aoû 2008, 13:12
par Euler911 » 30 Aoû 2008, 13:12
Il y a des erreurs dans ton système...
-
mythos75
- Membre Naturel
- Messages: 35
- Enregistré le: 11 Aoû 2008, 15:34
-
 par mythos75 » 30 Aoû 2008, 13:16
par mythos75 » 30 Aoû 2008, 13:16
Oups.
Eq. de la droite : ?
x = -1 -k
y = 2 + 2k
z = 3 - 4k
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 30 Aoû 2008, 13:18
par Euler911 » 30 Aoû 2008, 13:18
Oui c'est ça!
Maintenant vérifie si C vérifie les équations param. de cette droite (c-à-d si tu trouves un seul et même k pour les 3 équations)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 82 invités
